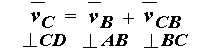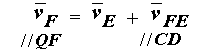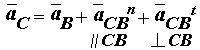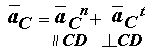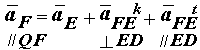Тема : Кинематический анализ рычажного механизма методом
построений планов положений, скоростей и ускорений
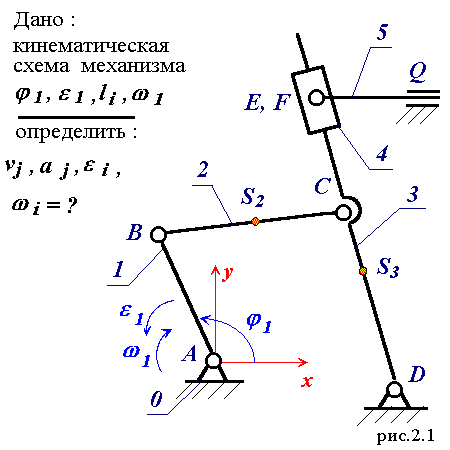
В данном примере приводится кинематический анализ шестизвенного механизма (рис.2.1). Решение векторных уравнений скоростей и ускорений проводится графическим методом, часть неизвестных определяется по уравнениям кинематики плоского движения аналитически. Таким образом для решения уравнений в задаче используется комбинированный графо-аналитический метод.
Построение планов положений, скоростей и ускорений.
Построение плана положений. Планом положений механизма называется векторная диаграмма, на которой в масштабе изображены в виде векторов звенья механизма. Кинематические пары на плане положений не изображаются. С помощью плана положений графически решается задача о положении звеньев, определяются неизвестные линейные и угловые координаты.
Построение плана скоростей. Определяем виды относительного движения звеньев: звено 5 движется поступательно, звенья 1, 3 совершают вращательное движение, а звенья 2, 4 - плоское.
Линейную скорость точки B звена 1 определяем по формуле :
Построение плана скоростей. Определяем виды относительного движения звеньев: звено 5 движется поступательно, звенья 1, 3 совершают вращательное движение, а звенья 2, 4 - плоское.
Линейную скорость точки B звена 1 определяем по формуле :
vB = w1 * lAB
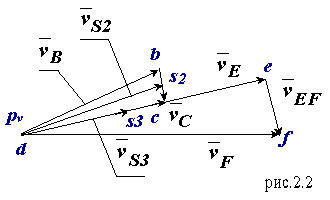
На плане (рис.2.2) скорость
vB изображается отрезком
pvb. Зададимся величиной этого отрезка и определим масштаб плана скоростей
mv = pvb / vB.
Для скорости точки
C составим векторное уравнение сложного движения
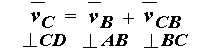
из графического решения которого находим модули векторов скоростей :
vC = pvc / mv
vBC = bc / mv
Скорости центров масс
S2 и
S3 , а также скорость точки
E звена 3 определяем пропорциональным делением отрезков плана скоростей :
BS2 / BC = bs2 / bc , bs2 = (BS2 / BC) * bc
DS3 / DC = ds3 / dc , ds3 = (DS3 / DC) * dc
DE3 / DC = de / dc , de = (DE3 / DC) * dc
Следовательно :
vS2 = bs2 / mv ,
vS3 = bs3 / mv ,
vE = de / mv .
Для скорости точки
F составим векторное уравнение сложного движения
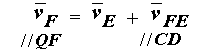
из графического решения которого находим модули векторов скоростей :
vF = pvf / mv
vEF = ef / mv
Угловые скорости звеньев 2 и 3 находим по формулам :
w2 = vCB / lCB
w3 = vC / lCD
План скоростей показан на рис.2.2.
 Построение плана ускорений
Построение плана ускорений. Ускорение точки B звена 1, совершающего вращательное движение, определяем по формуле.
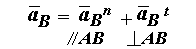
где
a B n = w12 * lAB - нормальная состовляющая ускорения ,
a Bt = e1 * lAB - тангенциальная состовляющая ускорения .
Задаемся величиной отрезка
pan'b , изображающего на плане ускорений нормальную составляющую, и определим масштаб плана ускорений ma = pan'b / aBn.
Ускорение точки C определяется совместным решением векторных уравнений сложного движения точки C относительно точки B.
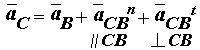
и вращательного движения точки C :
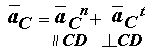
где
aСBn = w22 * lBC , aCn = w32 * lCD
Тангенциальные состовляющие найдем из плана ускорений :
aCBt = n'cbc' / ma , aCt = n'cc' / ma
Ускорение центров масс S2 , S3 и точки E определим методом пропорционального деления отрезков плана ускорений :
BS2 / BC = b's2' / b'c' , b's2' = (BS2 / BC) * b'c'
DS3 / DC = d's3' / d'c' , d's3' = (DS3 / DC) * d'c'
DE3 / DC = d'e' / d'c' , d'e' = (DE3 / DC) * d'c'
Следовательно
: aS2 = b's2' / ma , aS3 = b's3' / ma , aE = d'e' / ma .
Для ускорения точки F составим векторное уравнение сложного движения :
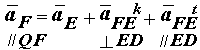
где
aFEk = 2 * w3 * vFE - ускорение Кариолиса точки F в относительном движении относительно точки E .
Угловые ускорения звеньев 2 и 3 определяем по формулам :
e2 = aCBt / lCB
e3 = aCt / lCD
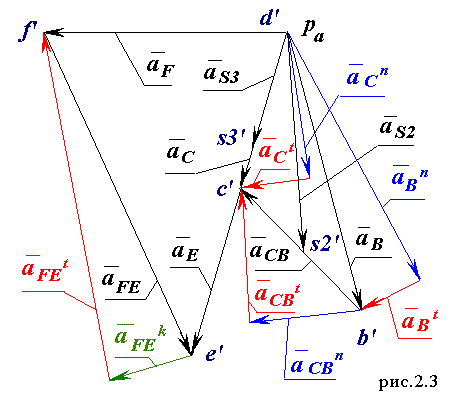
Итак, с помощью графо - аналитического метода, мы определели угловые скорости и ускорения звеньев , а также линейные скорости и ускорения заданных точек механизма, изображенного на рис.2.1.
Использован материал с сайта:
http://tmm-umk.bmstu.ru/seminar/sem2.htm