Тема : Кинематическое исследование рычажного механизма 
аналитическим методом (метод проекций векторных контуров)

При кинематическом исследовании механизма методом проекций векторных контуров схема механизма заменяется эквивалентной смстемой векторов, которые определяют положение звеньев и точек механизма относительно базовой системой координат xAy. При решении задачи из этой системы выделяют простые векторные контуры, содержащие не более двух неизвестных, и рассматривают эти контуры в проекциях на оси координат. Далее, в зависимости от поставленной задачи, определяются геометрические (передаточные функции) или кинематические (скорости и ускорения) параметры механизма. В первом случае дифференцирование уравнений проекций векторных контуров проводится по обобщенной координате, во втором - по времени. Рассмотрим пример кинематического анализа шестизвенного рычажного механизма (рис.3.1) методом проекций векторных контуров.

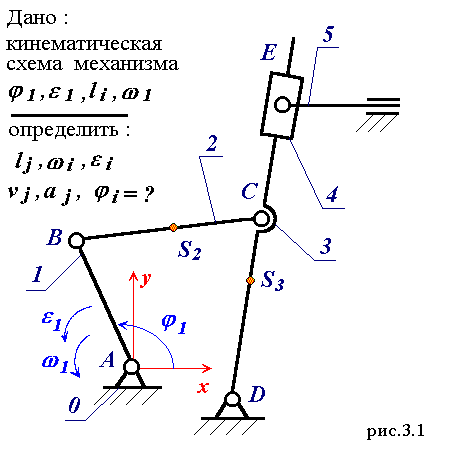
 Эквивалентная система векторных контуров для этого механизма изображена на рис.3.2

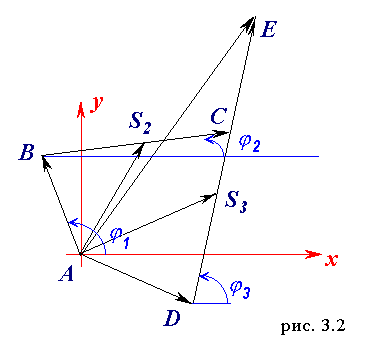
Векторный контур, определяющий положение точки B.


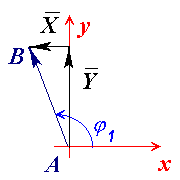
Положение точки B относительно начала ситемы координат можно описать следующим векторным уравнением :


Проекции этого контура на оси координат :
x_B = l_AB * cos(j₁)
y_B = l_AB * sin(j₁)

Первая и вторая производная от этих уравнений по времени :
v_Bx = - l_AB * w₁ * sin(j₁)
v_By = l_AB * w₁ * cos(j₁)

a_Bx = - l_AB * e₁ * sin(j₁) - l_AB * w₁² * cos(j₁)
a_By = l_AB * e₁ * cos(j₁) - l_AB * w₁² * sin(j₁) 

Скорость и ускорение точки B :


Векторный контур, определяющий положение точки C.

Положение точки C относительно начала ситемы координат можно описать следующим векторным уравнением :


Проекции этого контура на оси координат :
x_C = l_AB * cos(j₁) + l_BC * cos(j₂) = x_D + l_DC * cos(j₃)
y_C = l_AB * sin(j₁) + l_BC * sin(j₂) = y_D + l_DC * sin(j ₃)

Из этой системы уравнений определяем угловые координаты звеньев   j2   и   j3 
Первая производная от этих координат по времени :

v_Cx = - l_AB * w₁ * sin(j₁) - l_BC * w₂ * sin(j₂) = - l_DC * w₃ * sin(j₃)
v_Cy = l_AB * w₁ * cos(j₁) + l_BC * w₂ * cos(j₂) = l_DC * w₃ * cos(j₃)

Из этой системы уравнений определяем угловые скорости звеньев   w₂   и   w₃ 
Координаты точки C найдем из системы уравнений :
x_C = x_D + l_DC * cos(j ₃)
y_C = y_D + l_DC * sin(j₃)

Линейную скорость точки C найдем найдем из системы уравнений :
v_Cx = = - l_DC * w₃ * sin(j₃)
v_Cy = l_DC * w₃ * cos(j₃)


Вторая производная для проекций рассматриваемого векторного контура :


a_Cx = a_Bx - l_BC * e ₂ * sin(j₂) - l_BC * w₂² * cos(j₂) = - l_DC * e₃ * sin(j₃) - l_DC * w₃² * cos(j₃)
a_Cy = a_By + l_BC * e ₂ * cos(j₂) - l_BC * w₂² * cos(j₂) = l_DC * e₃ * cos(j₃) - l_DC * w₃² * sin(j₃) 

Из этой системы уравнений определяем угловые ускорения звеньев   e₂   и   e₃, а также линейное ускорение точки C :


Векторный контур, определяющий положение точки S3.

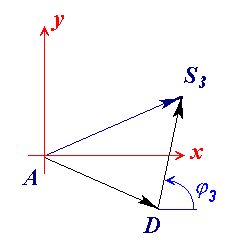
Положение точки S3 относительно начала ситемы координат можно описать следующим векторным уравнением :


Проекции этого контура на оси координат :
x_S3 = x_D + l_DS3 * cos(j₃)
y_S3 = y_D + l_DS3 * sin(j₃)

Первая и вторая производная от этих уравнений по времени :
v_S3x = - l_DS3 * w₃ * sin(j₃)
v_S3y = l_DS3 * w₃ * cos(j₃)

a_S3x = - l_DS3 * e₃ * sin(j₃) - l_DS3 * w₃² * cos(j₃)
a_S3y = l_DS3 * e₃ * cos(j₃) - l_DS3 * w₃² * sin(j₃)

Скорость и ускорение точки S3 :


Векторный контур, определяющий положение точки S2.

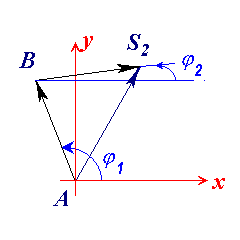
Положение точки S2 относительно начала ситемы координат можно описать следующим векторным уравнением :


Проекции этого контура на оси координат :
x_S2 = l_AB * cos(j₁) + l_BS2 * cos(j₂)
y_S2 = l_AB * sin(j₁) l_BS2 * sin(j₂)

Первая и вторая производная от этих уравнений по времени :
v_S2x = - l_AB * w₁ * sin(j₁) - l_BS2 * w₂ * sin(j₂)
v_S2y = l_AB * w₁ * cos(j₁) + l_BS2 * w₂ * cos(j₂)

a_S2x = - l_AB * e₁ * sin(j₁) - l_AB * w₁² * cos(j₁) - l_BS2 * e₂ * sin(j₂) - l_BS2 * w₂² * cos(j₂)
a_S2y = l_AB * e₁ * cos(j₁) - l_AB * w₁² * sin(j₁) + l_BS2 * e₂ * cos(j₂) - l_BS2 * w₂² * sin(j₂)

Скорость и ускорение точки S2 :


Векторный контур, определяющий положение точки E.

Положение точки E относительно начала ситемы координат можно описать следующим векторным уравнением :


Проекции этого контура на оси координат :
x_E = x_D + l_DE * cos(j₃)
y_E = y_D + l_DE * sin(j₃)

Первая и вторая производная от этих уравнений по времени :
v_Ex = v_DE * cos(j₃) - l_DE * w₃ * sin(j₃) = v _E
v_Ey = v_DE * sin(j₃) + l_DE * w₃ * cos(j₃) = 0

a_Ex = a_DE * cos(j₃) - 2 * v_DE * w₃ * sin(j₃) - l_DE * e₃ * sin(j₃) - l_DE * w₃² * cos(j₃) = a_E
a_Ey = a_DE * sin(j₃) + 2 * v_DE * w₃ * cos(j₃) + l_DE * e₃ * cos(j₃) - l_DE * w₃² * sin(j₃) = 0

Скорость и ускорение точки E :


Итак, с помощью метода проекции векторных контуров, мы определили угловые скорости и ускорения звеньев , а также линейные скорости заданных точек механизма, изображенного на рис.3.1.

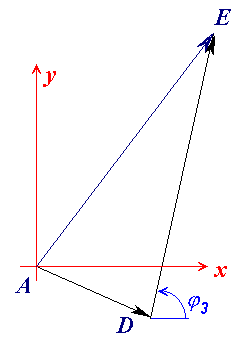
Использован материал с сайта: http://tmm-umk.bmstu.ru/seminar/sem3.htm