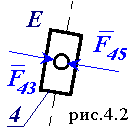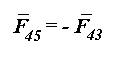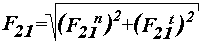Рассматривается кинетостатический расчет шестизвенного рычажного механизма (рис.4.1). Решение поставленной задачи осуществляется методом кинетостатики. Решение векторных уравнений сил проводится графическим методом, а уравнения моментов решаются аналитически. Таким образом в данном примере для решения уравнений кинетостатики используется графо-аналитический метод.
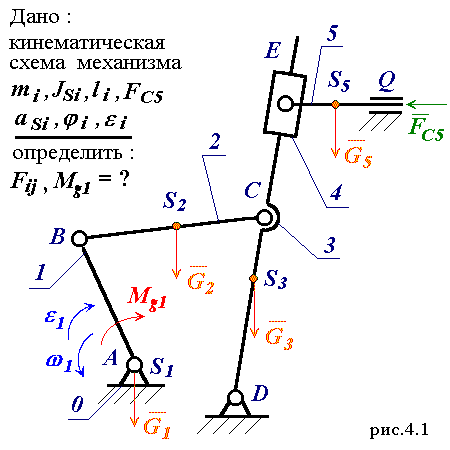 Уравнения кинестатического равновесия :
S Fi + S FФi = 0 , S Mi + S MФi = 0
Уравнения кинестатического равновесия :
S Fi + S FФi = 0 , S Mi + S MФi = 0
где
FФi - инерционные силы, приложенные к звеньям
, MФi - моменты сил инерции, приложенные к звеньям.
1. Определение числа неизвестных при силовом расчете .
Для определения числа неизвестных, а, следовательно, и числа независимых уравнений, при силовых расчетах необходимо провести структурный анализ механизма и определить число и классы кинематических пар, число основных подвижностей, число избыточных связей. Чтобы силовой расчет можно было провести, используя только уравнения кинетостатики, необходимо устранить в нем избыточные связи. В противном случае, к системе уравнений кинетостатики необходимо добавить уравнения деформации звеньев, необходимые для раскрытия статической неопределимости механизма. Так как каждая связь в КП механизма соответствует одной компоненте реакции, то число неизвестных компонент равно суммарному числу связей накладываемых КП механизма. Уравновешивающая сила или момент должны действовать по каждой основной подвижности механизма. Поэтому суммарное число неизвестных в силовом расчете определяется суммой связей в КП механизма и его основных подвижностей .
ns = W0 + S (H-i) * pi
где
ns - число неизвестных в силовом расчете.
2. Определение сил тяжести.
Gi = mi * gi
3. Определение главных векторов и главных моментов сил инерции.
Фi = - mi * aSi
MФi = - ISi * ei
4. Кинетостатический силовой расчет механизма.
4.1. Силовой расчет группы звеньев 4 - 5.
В начале рассмотрим звено 4 (рис.4.2).
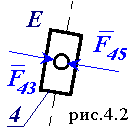
и запишем векторное уравнение сил :
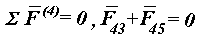
Из этого уравнения следует, что сила
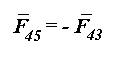
и приложена в точке
E к звену 4.
Сумма моментов для звена 4 относительно точки
E позволяет вычислить момент в поступательной паре
E, образованный звеньями 4 и 3,
S ME(4) = 0 , M43 = 0
Рассмотрим группу звеньев 4 - 5 :
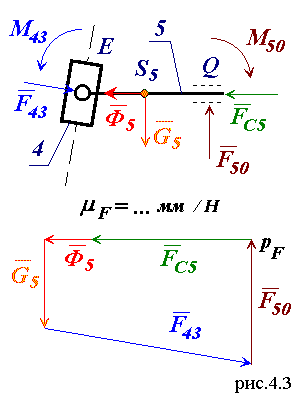
Векторное уравнение сил для группы звеньев 4 - 5 (рис.4.3) дает возможность определить модули векторов сил
F43 и F50.
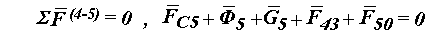
Строим план сил в масштабе
m F и находим
F43 = ab / m F
F50 = bpF / m F
Для определения реактивного момента в поступательной паре
Q составим уравнение моментов для звенев 4 - 5 относительно точки
Q
S MQ(4 - 5) = 0
- M50 + F43 * hQF43 + G5 * lS5Q = 0
из последнего уравнения определяем
M50 .
4.2. Силовой расчет группы звеньев 2 - 3.
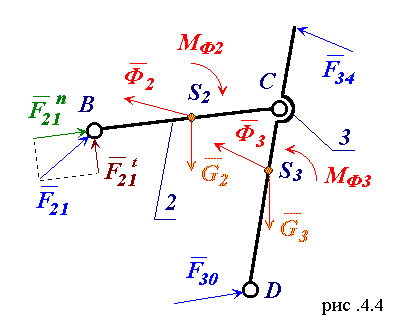
В начале рассмотрим звено 2 :
S MC(2) = 0
- MФ2 + G2 * hCG2 - Ф2 * hCФ2 - F21t * lBC = 0
Из этого уравнения определяем тангенсальную состовляющую
F21t .
Рассмотрим сумму моментов для группы звеньев 2 - 3 относительно точки
D :
- MФ2 + G2 * hDG2 + Ф2 * hDФ2 + MФ3 - F21t * hDF21t - F21n * hDF21n - G3 * hDG3 + Ф3 * hDФ3 = 0
Из этого уравнения определяем нормальную составляющую
F21n .
Полная реакция в паре
B равна
:
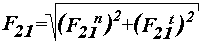
Векторное уравнение сил для группы 2 - 3 позволяет графически определить вектор F30 по величине и направлению (рис.4.5).
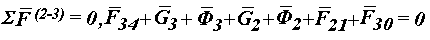
Строим план сил в масштабе mF (рис.4.5) и находим F30 = cpF / mF .
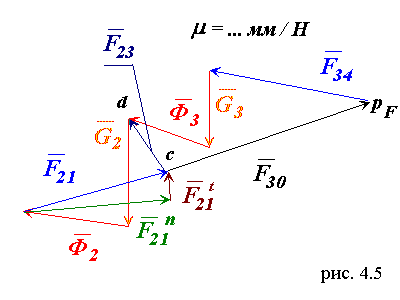
Рассмотрим векторное уравнение сил (рис.4.5) для звена 2 :
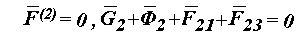
Из которого находим
: F23 = dc / mF
4.3. Силовой расчет начального звена 1 (рис.4.6).
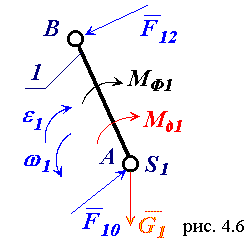
Из векторного уравнения сил для звена 1 графически определяем вектор
F10 по величине и направлению:
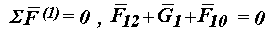
Строим план сил (рис.4.7) в масштабе
m F и находим
F10 = cpF / m F
Сумма моментов для звена 1 относительно точки
A дает возможность найти значение движущего момента
Mд1 :
S MA(1) = 0
- F12 * hAF12 + Mд1 + MФ1 = 0
Итак, с помощью графо - аналитического способа мы определили величины и направления реакций в кинематических парах, величины реактивных моментов и значение уравновешивающего момента данного механизма.
Использован материал с сайта: http://tmm-umk.bmstu.ru/seminar/sem4.htm