Зубчатые колеса

Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев. При проектировании зубчатого колеса вначале нужно определить его число зубьев z, а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса r_y разделить на z частей, каждая из которых называется окружным шагом p_y.

2 * p * r_y = p_y * z
2 * r_y = ( p_y / p ) * z = m_y * z = d_y

где m_y = p_y / p = d_y / z - модуль зацепления по окружности произвольного радиуса.

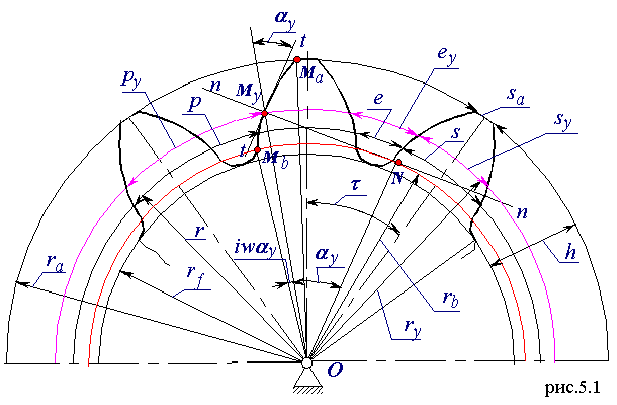 Модулем зацепления называется линейная величина в p  раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к p, то есть модуль - число миллиметров диаметра приходящееся на один зуб.
Делительная окружность - окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение.
Шаг p - расстояние по дуге окружности между одноименными точками профилей соседних зубьев.
Угловой шаг t - центральный угол соответствующий дуге p - окружному шагу по делительной окружности.
Угол профиля a - острый угол между касательной к профилю в данной точке и радиусом - вектором, проведенным в данную точку из центра колеса.
Шаг колеса делится на толщину зуба s_y и ширину впадины e_y.
Толщина зуба s_y - расстояние по дуге окружности ry между разноименными точками профилей зуба. 
Ширина впадины e_y - расстояние по дуге окружности r_y между разноименными точками профилей соседних зубьев.
Инвалюта - угол развернутости эвольвенты.

Понятие об исходном, исходном производящем и производящем контурах.
Для сокращения номенклатуры режущего инструмента стандарт устанавливает нормативный ряд модулей и определенные соотношения между размерами элементов зуба. Эти соотношения определяются :

• для зубчатых колес определяются параметрами исходной рейки через параметры ее нормального сечения - исходный контур ;
  
• для зубчатого инструмента определяются параметрами исходной производящей рейки через параметры ее нормального сечения - исходный производящий контур (рис.5.2);

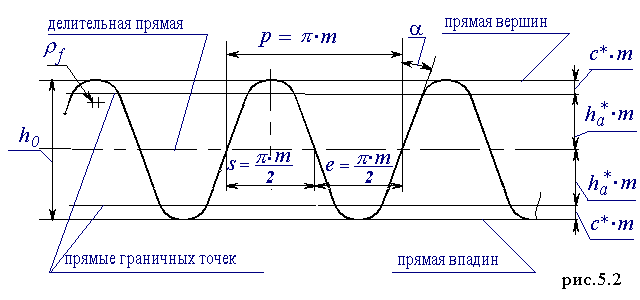
По ГОСТ 13755-81 значения параметров исходного контура должны быть следующими :

• угол главного профиля a = 20 ⁰ ;
• коэффициент высоты зуба h^*_a = 1 ;
• коэффициент высоты ножки h^*_f = 1.25 ;
• коэффициент граничной высоты h^*_l = 2 ;
• коэффициент радиуса кривизны переходной кривой r ^*_f = c^* / ( 1 - sina ) = 0.38 ;
• коэффициент радиального зазора в паре исходных контуров c^* = 0.25 .

Исходный производящий контур отличается от исходного высотой зуба h₀ = 2.5m.
Производящий контур - проекция режущих кромок инструмента на плоскость перпендикулярную оси заготовки.

Станочное зацепление.
Станочным зацеплением называется зацепление, образованное заготовкой колеса и инструментом, при изготовлении зубчатого колеса на зубообрабатывающем оборудовании по способу обката. Схема станочного зацепления колеса и инструмента с производящим контуром, совпадающим с исходным производящим контуром, изображена на рис.5.3.



Линия станочного зацепления - геометрическое место точек контакта эвольвентной части прфиля инструмента и эвольвентной части профиля зуба в неподвижной системе координат.
Смещение исходного производящего контура x * m - кратчайшее растояние между делительной окружностью заготовки и делительной прямой исходного производящего контура.
Уравнительное смещение Dy * m - условная рассчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении ( величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора ).
Окружность граничных точек r_l - окружность проходящая через точки сопряжения эвольвентной части профиля зуба с переходной кривой.

Классификация зубчатых колес по величине смещения.
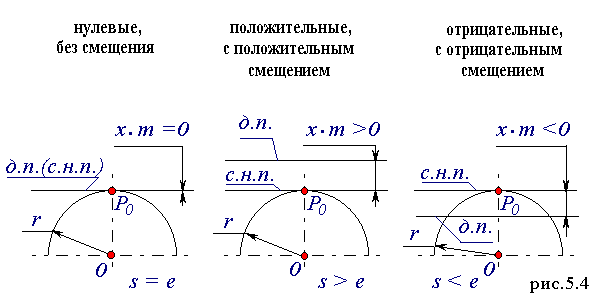
В зависимости от расположения исходного производящего контура относительно заготовки зубчатого колеса, зубчатые колеса делятся на нулевые или без смещения, положительные или с положительным смещением, отрицательные или с отрицательным смещением (рис.5.4).



Цилиндрическая эвольвентная зубчатая передача.
Два зубчатых колеса с одинаковым модулем и с числами зубьев соответствующими заданному передаточному отношению образуют зубчатую передачу или простейший зубчатый механизм. В этом трехзвенном механизме зубчатые колеса образуют между собой высшую пару, а со стойкой низшие пары.Зубчатая передача, кроме параметров образующих ее колес, имеети собственные параметры : угол зацепления a_w, межосевое расстояние a_w, воспринимаемое смещение y * m, и уравнительное смещение Dy * m. Передаточное отношение механизма u₁₂, числа зубьев колес z₁ и z₂, начальные окружности r_w1 и r_w2 ( или центроиды ) и межосевое расстояние a_w связаны между собой следующими соотношениями :
a_w = r_w1 + r_w2 ;       u₁₂ = r_w2 / r_w1 ;       a_w = r_w1 * ( 1 + u₁₂ ) ;
r_w1 = a_w / ( 1 + u₁₂ ) ;       r_w2 = r_w1 - a_w .

Изобразим схему зацепления эвольвентной зубчатой передачи (рис.5.5).

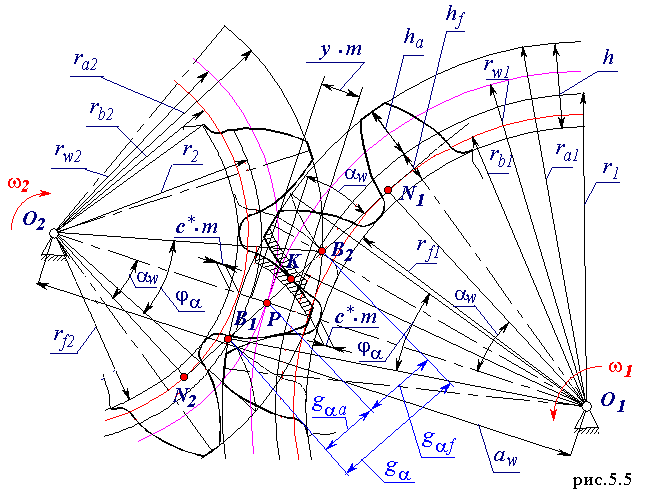Межосевое расстояние a_w - кратчайшее расстояние между осями колес.
g - линия зацепления ( N₁N₂ ).
g_a - активный участок линии зацепления ( B₁B₂ ).
g_a f - активный участок линии зацепления, соответствующий контакту на ножке зуба ведущего колеса.
g_a a - активный участок линии зацепления, соответствующий контакту на головке зуба ведущего колеса.
Полюс зацепления P - мгновенный центр относительного вращения звеньев, образующих кинематическую пару.
Угол зацепления a_w - острый угол между касательной к профилю в данной точке и радиусом - вектором, проведенным в данную точку из центра колеса.
Угол перекрытия j_a w - угол на который повернется колесо за время зацепления одной пары зубьев.
Коэффициент торцевого перекрытия e_a - величина отношения угла перекрытия к его угловому шагу.
e_a = j_a   /  t = l_B1B2  /  p_B ; 

Воспринимаемое смещение y * m - кратчайшее расстояние между делительными окружностями зубчатых колес.
Примечание : Более подробно познакомиться с основными определениями и рассчетными зависимостями можно в лекциях по курсу ТММ №12, №13. 
Использован материал с сайта: http://tmm-umk.bmstu.ru/seminar/sem5.htm