Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным или параллельным соединением простейших типовых зубчатых механизмов.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются
планетарными механизмами.
Элементы планетарного механизма имеют специальные названия:
- Зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";
- колесо с внутренними зубьями называют "короной" или "эпициклом";
- колеса, оси которых подвижны, называют "сателлитами";
- подвижное звено, на котором установлены сателлиты, называют "водилом".Звено водила принято обозначать не цифрой, а латинской буквой h.
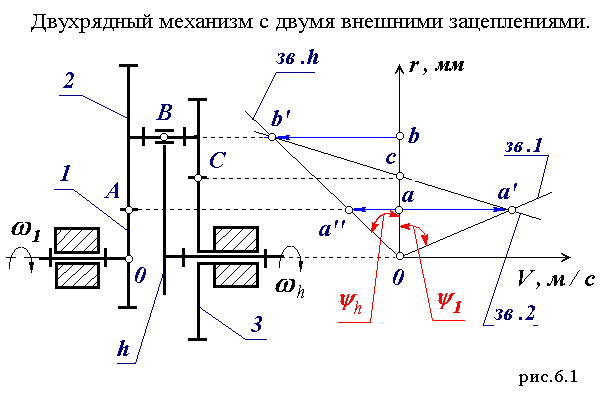
На рис.6.1 изображен типовой планетарный двухрядный механизм с двумя внешними зацеплениями.
 Аналитическое определение передаточного отношения.
Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис.6.1 на звене 2 нарезаны два зубчатых венца :
z2 , который зацепляется с зубчатым венцом
z1 звена 1
;
z3 , который зацепляется с внутренним зубчатым венцом
z4 звена 3
.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес
z2 и
z1
( w1 - wh ) / ( w2 - wh ) = - z2 / z1 ;
для внешнего зацепления колес
z4 и
z3
( w2 - wh ) / ( w3 - wh ) = - z4 / z3 ;
Перемножим, правые и левые части этих уравнений, и получим
[ ( w1 - wh ) / ( w2 - wh ) ] * [( w2 - wh ) / ( w3 - wh ) ] = z2 * z4 / z1 * z3 ;
[ ( w1 - wh ) / ( - wh ) ] = z2 * z4 / z1 * z3 ;
u1h(3) = w1 / wh = 1 - z2 * z4 / z1 * z3
Графическое определение передаточного отношения.
В системе координат
ri0V построим треугольники распределения линейных скоростей звеньев. Для этого из точки
a c ординатой
r1 в выбранном произвольном масштабе
mV , мм / м * с-1отложим отрезок
aa'. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси
ri . Эта прямая образует с осью
ri угол
y1 . Так как в точке c скорости звеньев 2 и 3 равны между собой и равны нулю, то соединяя точку с прямой с точкой
a, получим линию распределения скоростей для звена 2. Так как точка
b принадлежит звеньям 2 и
h, то ее скорость определяется по лучу
сa' для радиуса равного
rB = ( r1 + r2 ), что в масштабе
mV , мм / м * с-1 соответствует отрезку
bb'. Соединяя точку
b' с началом координат прямой, найдем линию распределения скоростей для водила
. Эта линия образует с осью
ri угол
yh . Передаточное отношение планетарного механизма определенное по данным графическим построениям можно записать так
u1h(3) = w1 / wh = tgy1 / tgyh = aa' / aa"
Рассмотрим задачу подбора чисел зубьев для планетарного механизма.
Условия подбора чисел зубьев.
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма :
- заданное передаточное отношение с требуемой точностью;
- соосность входного и выходного валов механизма;
- свободное размещение (соседство) сателлитов;
- сборку механизма при выбранных числах зубьев колес;
- отсутствие подреза зубьев с внешним зацеплением;
- отсутствие заклинивания во внутреннем зацеплении;
- минимальные относительные габариты механизма.
Рассмотрим эти условия подробнее на примере двухрядного планетарного механизма с двумя внешними зацеплениями.
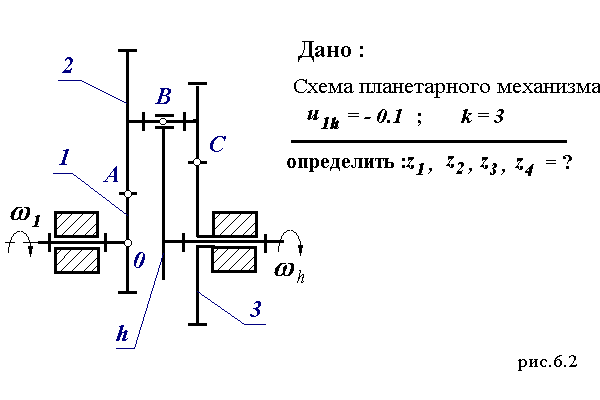
Для решения этой задачи используем метод сомножителей. Зубья колес планетарного механизма, рассчитанные этим методом, удовлетворяют условиям 1, 2, 5 и 6. Проверяем эти зубья по условиям 3 (соседство) и 4 (сборки) и если они выполняются, считаем этот вариант одним из возможных решений. Если после перебора рассматриваемых сочетаний сомножителей получим несколько возможных решений, то проводим их сравнение по условию 7. Решением задачи будет сочетание чисел зубьев, обеспечивающее габаритный минимальный размер
R.
Передаточное отношение данного механизма :
u1h = 1 - z2 * z4 / z1 * z3
1 / 10 = 1 - z2 * z4 / z1 * z3
z2 * z4 / z1 * z3 = B * D / A * C = 11 / 10
11 / 10 = 1 * 11 / 2 * 5 = 11 * 1 / 5 * 2 = 11 * 1 / 2 * 5 = 1 * 11 / 5 * 2
Условие соосности для этой схемы :
z1 + z2 = z3 + z4
и выразим его через сомножители
a * (A + B) = b * (C + D).
Принимаем коэффициенты a и b
a = (D + C), b = (A + B),
И получаем для первого сочетания сомножителей :
z1 = (D + C) * A * q = (11 + 5) * 2 * q = 32 *q ;
z2 = (D + C) * B * q = (11 + 5) * 1 * q = 16 *q ;
z3 = (A + B) * C * q = (2 + 1) * 5 * q = 15 *q ;
z4 = (A + B) * D * q = (2 + 1) * 11 * q = 33 *q ;
при q = 2 : z1 = 64 , z2 = 32 , z3 = 30 , z4 = 66
Проверка условия соседства
sin( p / k ) > max[ ( z2,3 +2 ) / ( z1 + z2 ) ];
0.866 > 0.375 - условие выполняется .
Проверка условия сборки
( u1h * z1 / k ) * ( 1 + k * p ) = B (целое число)
(- 32 / 10 * 3 ) * ( 1 + 3 * p ) - не целое число, условие сборки не выполняется. Следовательно рассмотрим второе сочетание сомножителей :
z1 = (D + C) * A * q = (1 + 2) * 5 * q = 15 *q ;
z2 = (D + C) * B * q = (1 + 2) * 11 * q = 33 *q ;
z3 = (A + B) * C * q = (5 + 11) * 2 * q = 32 *q ;
z4 = (A + B) * D * q = (5 + 11) * 1 * q = 16 *q ;
при q = 2 : z1 = 30 , z2 = 66 , z3 = 64 , z4 = 32
Проверка условия соседства
sin( p / k ) > max[ ( z2,3 +2 ) / ( z1 + z2 ) ];
0.866 > 0.708 - условие выполняется .
Проверка условия сборки
( u1h * z1 / k ) * ( 1 + k * p ) = B (целое число)
(- 30 / 10 * 3 ) * ( 1 + 3 * p ) = B - целое число, условие выполняется. То есть, получен первый вариант решения.
Габаритный размер : R = min [ max ( z1 + 2 * z2 ) ] = 81
Рассмотрим третье сочетание сомножителей :
z1 = (D + C) * A * q = (1 + 5) * 2 * q = 12 *q ;
z2 = (D + C) * B * q = (1 + 5) * 11 * q = 66 *q ;
z3 = (A + B) * C * q = (2 + 11) * 5 * q = 65 *q ;
z4 = (A + B) * D * q = (2 + 11) * 1 * q = 13 *q ;
при q = 2 : z1 = 24 , z2 = 132 , z3 = 130 , z4 = 26
Проверка условия соседства
sin( p / k ) > max[ ( z2,3 +2 ) / ( z1 + z2 ) ];
0.866 > 0.858 - условие выполняется .
Проверка условия сборки
( u1h * z1 / k ) * ( 1 + k * p ) = B (целое число)
(- 24 / 10 * 3 ) * ( 1 + 3 * p ) - не целое число, условие не выполняется. Рассмотрим последнее сочетание сомножителей :
z1 = (D + C) * A * q = (11 + 2) * 5 * q = 65 *q ;
z2 = (D + C) * B * q = (11 + 2) * 1 * q = 13 *q ;
z3 = (A + B) * C * q = (5 + 1) * 2 * q = 12 *q ;
z4 = (A + B) * D * q = (5 + 1) * 11 * q = 66 *q ;
при q = 2 : z1 = 130 , z2 = 26 , z3 = 24 , z4 = 132
Проверка условия соседства
sin( p / k ) > max[ ( z2,3 +2 ) / ( z1 + z2 ) ];
0.866 > 0.179 - условие выполняется .
Проверка условия сборки
( u1h * z1 / k ) * ( 1 + k * p ) = B (целое число)
(- 130 / 10 * 3 ) * ( 1 + 3 * p ) - не целое число, условие не выполняется.
Следовательно, только второе сочетание сомножителей удовлетворяет заданным условиям.
Ответ : z1 = 30 , z2 = 66 , z3 = 64 , z4 = 32

