η
Дано: вращающий момент на выходном валу Тв = 162000 Н-мм.
Найти диаметр промежуточного вала для участка передачи, схема которого изображена на рис. 13.
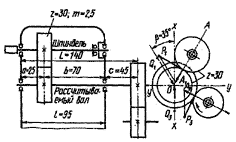
Рис. 13. Схема передачи к примеру для расчета
• Решение примера приведено в табл. 11.
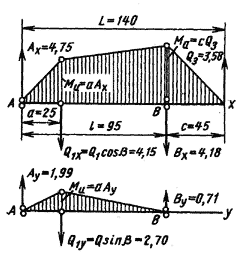
Рис. 14
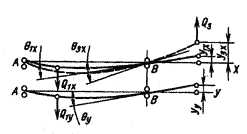
Рис. 15
11. Решение примера
| Определяемое | Расчетная формула | Расчет | |
| Вращающий момент с учетом η |
T = Tвi1/ h | h =0,96 T = (162000 · 1)/0,96 = 169 000 H·мм |
|
| Окружная сила | P = 2T/D | P1 = (2 · 169 000)/75 = 4,50 kH P3 = (2 · 169 000)/104 = 3,25 kH |
|
| Силы, действующие на вал и подшипники | Q » 11,1P | Q1 = 1,1 · 4,50 = 4,95 kH Q3 = 1,1 · 3,25 = 3,58 kH |
|
| Реакция опоры в плоскости х и у с учетом знака (рис.14) |
Опора А | Ax = (bQ1cosb) + cQ3/l | Ax = + 70/95 · 4,95 · 0,839 + + 45/95 · 3,58 = 4,75 кН |
| Реакция опоры в плоскости х и у с учетом знака (рис.14) |
Опора А | Ay = (bQ1sinb)/l | Ay = + 70/95 · 4,95 · 0,545 = 1,99 кН |
| Опора В | Bx = (aQ1cosb)/l - LQ3/l | Bx = + 25/95 · 4,95 · 0,839 - + 140/95 · 3,58 = -4,18 кН |
|
| By = (aQ1sinb)/l | By = + 25/95 · 4,95 · 0,545 = 0,71 кН |
||
| Полная реакция | Опора А | A = Ö(Ax2 + Ay2) | A = Ö(4,752 + 1,992) = 5,15 кН |
| Опора В | B = Ö(Bx2 + By2) | B = Ö(4,182 + 0,712) = 4,22 кН |
|
| Изгибающий момент в опасном сечении (рис.14) |
Плоскости х, у | См. эпюры (рис.14) | Опасное сечение в опоре В |
| Суммарный | Mи = Ö(Mих2 + Mиy2) | Mи = Mих = 161000 Hмм |
|
| Отношение Т/Ми в опасном сечении | Т/Ми | 169000 : 161000 = 1,05 |
|
| Диаметр вала (по Ми, Н м, и Т/Ми) | По таблице 10 | d =30 мм |
|
| Угол наклона упругой линии в расчетном сечении в плоскости х |
Отдельно от каждой силы |
qnx = (KqQnxl2)/(104 · d4) где l и d - в см |
q3x = (3,58 · 90) / (104 · 81) · 1,7 = = 0,00068 рад q1x = (4,15 · 90) / (104 · 81) · 0,4 = = 0,00018 рад |
| Суммарный | qx = å qnx | θ х = 0,00068+ + 0,00018 = 0,00086 |
|
| Угол наклона упругой линии в расчетном сечении в плоскости у (рис. 15) |
qny = (KqQnyl2)/(104 · d4) qy = å qny |
q1y = (2,70 · 90) / (104 · 81) · 0,4 = = 0,00012 рад qy = q1y = 0,00012 рад |
|
| Угол наклона упругой линии в расчетном сечении |
q = Ö(qx2 + qy2) | q = 10-5Ö(862 + 122) = 0,00087 рад |
|
| Прогиб в расчетном сечении в плоскости х |
Отдельно от каждой силы |
ynx = (KyQnxl3)/(104 · d4) где d и l - в см |
y3x = (3,58 · 856) / (104 · 81) · 1,2 = = 0,00045 см y1x = с · tgq1x = 4,5 x x 0,00018 = 0,0008 см |
| Суммарный | Ух= 0,0045 + 0,0008 = 0,0053 |
||
| То же, в плоскости у (рис. 15) | yny = (KyQxyl3)/(104 · d4) |
||
yy = å yny |
yy = с · tgqy = 4,5 x x 0,00012 = 0,0005 см |
||
| Прогиб в расчетном сечении | y = Ö(yx2 + yy2) | y = 10-4Ö(532 + 52) » 0,0053 см |
|
| Допустимые величины | θ в опоре | 0,001 | 0,00087 рад |
| Умах, СМ | 0,0001 + 0,0005 = ymax/l ymax = (0,01 + 0,03)m m - модуль в см |
0,0053 : 9,5 = 0,00056; ymax = 0,03 · 0,25 = 0,0075 ymax = 0,03 · 0,25 = 0,0075 фактически 0,0053 |
|
Примечание. В отношении жесткости вала диаметр d=30 мм допустим. Для создания лучших условий работы подшипников и зубчатых колес следует принять d=32 мм.
12. Сравнение сплошных и полых валов различного сечения
но наружному диаметру (d, d1)моменту инерции (J, J1),
моменту сопротивления (W, W1) и массе (площади поперечного сечения F, F1)

J1/J, и W1 /W - относительные значения моментов инерции и моментов сопротивления сечений полых валов как при изгибе, так и при кручении.
| d2 d1 |
При одинаковом наружномдиаметре валов d1=d |
При одинаковой массе валов или при одинаковой площади сечения F=F1 |
При одинаковой прочности валов W1=W1 |
При одинаковой жесткости валов J=J1 |
||||||
|
J1/J = |
Умень- |
d1 d |
J1 J |
W1 W |
d1/d = = J1/J |
Умень- шение массы, % |
d1 d |
W1 W |
Умень- шение массы, % |
|
| 0,1 0,2 0,3 0,4 0,5 0,6 |
1,000 0,998 0,992 0,974 0,938 0,870 |
1 4 9 16 25 36 |
1,01 1,02 1,05 1,09 1,15 1,25 |
1,020 1,083 1,198 1,381 1,667 2,13 |
1,015 1,061 1,142 1,265 1,443 1,70 |
1,000 1,001 1,003 1,009 1,021 1,047 |
1 4 9 14 22 30 |
1,00 1,00 1,00 1,01 1,02 1,04 |
1,000 1,000 0,998 0,994 0,984 0,966 |
1 4 9 15 23 31 |