Определение сил, нагружающих подшипники

Определение радиальных реакций. Вал на подшипниках, установленных по одному в опоре, условно рассматривают как балку на шарнирно-подвижных опорах или как балку с одной шарнирно-подвижной и одной шарнирно-неподвижной опорой. Радиальную реакцию F_r подшипника считают приложенной к оси вала в точке пересечения с ней нормалей, проведенных через середины контактных площадок. Для радиальных подшипников эта точка расположена на середине ширины подшипника. Для радиально-упорных подшипников расстояние а между этой точкой и торцом подшипника может быть определено графически (рис. 25) или аналитически:
подшипники шариковые радиально-упорные однорядные

a=0,5[B+0,5(d+D))tgα];

подшипники роликовые конические однорядные

a=0,5(T+(d+D)е/з].

Ширину В кольца, монтажную высоту Т, коэффициент е осевого нагружения, угол

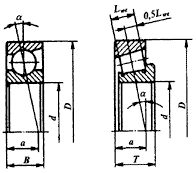
Рис.25.Расположение точки приложения
 радиальной реакции в радиально-упорных
 подшипниках

α контакта, а также диаметры d и D принимают по каталогу.
Реакции опор определяют из уравнения равновесия: сумма моментов внешних сил относительно рассматриваемой опоры и момента реакции в другой опоре равна нулю.

В ряде случаев направление вращения может быть переменным или неопределенным, причем изменение направления вращения может привести к изменению не только направления, но и значений реакций опор. При установке на концы валов соединительных муфт направление силы на вал от муфты неизвестно. В таких случаях при расчете реакций рассматривают наиболее опасный вариант. Возможная ошибка при этом приводит к повышению надежности.

Определение осевых реакций. При установке вала на двух радиальных шариковых или радиально-упорных подшипниках нерегулируемых типов осевая сила F_a, нагружающая подшипник, равна внешней осевой силе F_A, действующей на вал. Силу F_A воспринимает тот подшипник, который ограничивает осевое перемещение вала под действием этой силы.

При определении осевых сил, нагружающих радиально-упорные подшипники регулируемых типов, следует учитывать осевые силы, возникающие под действием радиальной нагрузки F_rвследствие наклона контактных линий. Значения этих сил зависят от типа подшипника, угла контакта, значений радиальных сил, а также от того, как отрегулированы подшипники (см. рис. 22,а-в). Если подшипники собраны с большим зазором, то всю нагрузку воспринимает только один или два шарика или ролика (рис. 22, а). Осевая составляющая нагрузки при передаче ее одним телом качения равна F_rtgα. Условия работы подшипников при таких больших зазорах неблагоприятны, и поэтому такие зазоры недопустимы. Обычно подшипники регулируют так, чтобы осевой зазор при установившемся температурном режиме был бы близок к нулю. В этом случае под действием радиальной нагрузки F_r находятся около половины тел качения (рис. 22, 6), а суммарная по всем нагруженным телам качения осевая составляющая из-за наклона контактных линий равна е' F_r и представляет собой минимальную осевую силу, которая должна действовать на радиально-упорный подшипник при заданной радиальной силе:

F _{a min} = е^' F_r                            (24)

  Для шариковых радиально-упорных подшипников с углом контакта а < 18°, F _{a min} = е^' F_r ,  где е' - коэффициент минимальной осевой нагрузки. В подшипниках такого типа действительный угол контакта отличается от начального и зависит от радиальной нагрузки F_r и базовой статической грузоподъемности С_or- Поэтому коэффициент е' определяют по формулам:
 для подшипников с углом контакта а = 12°

е^'= 0,563(F _r/C_or) ^0,195;       (25)
 

 для подшипников с углом контакта а = 15°

е^'= 0,579(F _r/C_or) ^0,136;       (26)
 

  Для шариковых радиально-упорных подшипников с углом контакта а ≥ 18°, е^'=e  и F _{a min} = е^' F_r . Значения коэффициента е  осевого нагружения принимают по таблице 64. 
  Для конических роликовых:  е^'= 0,83e   и F _{a min} = 0,83 е F_r . Значения коэффициента е  принимают по каталогу.
 Под действием силы F _{a min} наружное кольцо подшипника поджато к крышке корпуса. При отсутствии упора кольца в крышку оно будет отжато в осевом направлении, что приведет к нарушению нормальной работы подшипника. Для обеспечения нормальных условий работы осевая сила, нагружающая подшипник, должна быть не меньше минимальной: F_а  ≥ F_а min . Это условие должно быть выполнено для каждой опоры.
 Если F_а  ≥ F_а min, то более половины или все тела качения подшипника находятся под нагрузкой (см. рис. 22, в). Жесткость опоры с ростом осевой нагрузки увеличивается, поэтому в некоторых опорах, например в опорах шпинделей станков, применяют сборку с предварительным натягом.
 Для нормальной работы радиально-упорных подшипников необходимо, чтобы в каждой опоре осевая сила, нагружающая подшипник, была бы не меньше минимальной:

 F_а1  ≥ F_а1 min и  F_а2  ≥ F_а2 min

 Кроме того, должно быть выполнено условие равновесия вала - равенство нулю суммы всех осевых сил, действующих на вал. Например, для схемы
по рис. 26 имеем

F_A + F_A1 ^_ F_A2= О.

Пример нахождения осевых реакций опор. В представленной на рис. 26 расчетной схеме обозначены: F_А и F_R - внешние осевая и радиальная нагрузки, действующие на вал; F_r1 и F_r2 -радиальные реакции опор; F_a1 и F_a2- осевые реакции опор.
 Решение может быть найдено при совместном удовлетворении трех уравнений:
 - из условия  F_а  ≥ F_а min в каждой опоре с учетом (24) следует:

F_а1  ≥ е^'₁ F_r1,     F_а2  ≥ е^' F_r2,     
- из условия  равновесия вала под действием осевых сил следует:

F_A + F_A1 ^_ F_A2= О.

Рис. 26. Схема нагружения вала и опор
 с радиально-упорными регулируемыми подшипниками

 Для нахождения решения применяют метод попыток, предварительно осевую силу в одной, из опор принимая равной минимальной.
 1. Пусть, например, F_а1  = е^'₁ F_r1. 
 Тогда из условия равновесия вала имеем

F_A2=F_A + F_а1= F_A +е^'₁ F_r1

 Проверяем выполнение условия F_а  ≥ F_а min для второй опоры. Если при этом F_а2  ≥ е'₂ F_r2 , то осевые силы найдены правильно. Если
 F_а2 < е'₂F_r2 (что недопустимо), то нужно предпринять вторую попытку.
 2. Следует принять: F_а2 = е'₂F_r2. Тогда из условия равновесия вала имеем

F_a1=F_a2 ^_ F_A=е^'₂ F_r2 ^_ F_A
 

 При этом условие F_а1  ≥ е'₁ F_r1 будет обязательно выполнено.