Цилиндрические косозубые передачи при параллельных валах

Косозубая передача более плавная и передает большую мощность, чем прямозубая, при тех же размерах. Недостатком косозу-бых передач является возникающая в зацеплении дополнительная осевая сила, отсутствующая у прямозубых колес. Линии зубьев имеют правое или левое направление. Правой называют такую линию, точка на которой движется по часовой стрелке при удалении вдоль зуба, если смотреть на колесо со стороны его торца (рис. 11). Углы наклона двух сцепляющихся колес равны. Схема развертки делительного цилиндра зубчатого колеса показана на рис. 12.

Рис. 11. Линии винтовых зубьев колес:
а - правая; б - левая

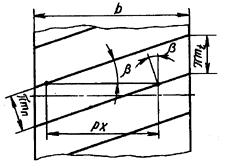
Рис. 12. Схема развертки делительного цилиндра косозубого колеса

10. Формулы и пример расчета косозубой передачи без смещении




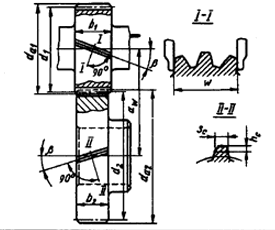
Если межосевое расстояние а
mn=4
z1 =41
z2 =82
a=250
b1 =32
b2=26
α =20°

Если межосевое расстояние а
не входит в исходные данные, то


 

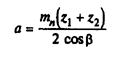
Параметры и обозначения

Расчетные формулы и указания

Числовые значения

 Угол наклона линии зуба ß
 Окружной (торцовый) модульmt

ß = 10°15'

 4,066

 Делительный диаметр d

d1= mt z1
d2= mt z2

166,706
333,412

 Диаметр вершин зубьев da

da1 = d1 + 2mn
da2 = d2 + 2mn

174,706
341,412

 Постоянная хорда ŝc


 или по табл. 11  ŝc= 1,387mn

5,55

 Высота до постоянной хорды ĥc

ĥc= 0,5( da- d - ŝc )tgα , где α = 20°, 
или по табл. 12   ĥc= 0,748mn

2,99
Расчет длины общей нормали

 Условное число зубьев zk

 zk1= Kz1;  по табл. 13 K=1,047;
zk2= Kz2
Если ß=0, то zT =z
42,927
85,854

 Часть длины общей нормали,
 определяемая целой частью zT
 величины  zk , выраженная в
 долях модуля

 W*T1 определяют по табл. 14,
W*T2- тоже по табл. 14.
Если ß=0, то zK =z		 13,8728 (при zn=5)
29,2357 (при zn=10)

 Часть длины общей нормали,
 определяемая дробной частью
 величины  zk , выраженная в
 долях модуля

 W*n1=0,0149(zK1-zT1)=0,0149(42,927-42);
W*n2=0,0149(zK2-zT2)=0,0149(85,854-85).
Если ß=0, то W*n=0		 0,0138
0,0127

 Длина обшей нормали W

 W1= (W*T1 + W*n1)m;
W2= (W*T2 + W*n2)m;
Для косозубых зубчатых колес должно выполняться дополнительное условие 

где b - ширина венца, sin ßb= sin ß cos α		 54,97
116,99




 

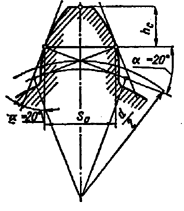
11. Значения постоянной хорды  ŝ*c  и расстояния ее от делительной окружности  ĥ*Δ, 
выраженные в долях модуля ( α= 20 °)

 

х

 ŝ*c 

ĥ*Δ

  

х

 ŝ*c 

ĥ*Δ

  

х

 ŝ*c 

ĥ*Δ

  

х

 ŝ*c 

ĥ*Δ

-0,50

1,0657

0,1940

-0,12

1,3099

0,2384

0,26

1,5542

0,2828

0,64

1,7984

0,3273

-0,49

1,0721

0,1951

-0,11

1,3164

0,2396

0,27

1,5606

0,2840

0,65

1,8049

0,3284

-0,48

1,0785

0,1963

-0,10

1,3228

0,2408

0,28

1,5670

0,2852

0,66

1,8113

0,3296

-0,47

1,0850

0,1975

-0,09

1,3292

0,2419

0,29

1,5735

0,2864

0,67

1,8177

0,3308

-0,46

1,0914

0,1986

-0,08

1,3356

0,2431

0,30

1,5799

0,2875

0,68

1,8241

0,3319

-0,45

1,0978

0,1998

-0,07

1,3421

0,2443

0,31

1,5863

0,2887

0,69

1,8306

0,3331

-0,44

1,1042

0,2010

-0,06

1,3485

0,2454

0,32

1,5927

0,2899

0,70

1,8370

0,3343

-0,43

1,1107

0,2021

-0,05

1,3549

0,2466

0,33

1,5992

0,2910

0,71

1,8434

0,3355

-0,42

1,1171

0,2033

-0,04

1,3614

0,2478

0,34

1,6056

0,2922

0,72

1,8498

0,3366

-0,41

1,1235

0,2045

-0,03

1,3678

0,2490

0,35

1,6120

0,2934

0,73

1,8563

0,3378

-0,40

1,1299

0,2057

-0,02

1,3742

0,2501

0,36

1,6185

0,2945

0,74

1,8627

0,3390

-0,39

1,1364

0,2068

-0,01

1,3806

0,2513

0,37

1,6249

0,2957

0,75

1,8691

0,3401

-0,38

1,1428

0,2080

0,00

1,3870

0,2524

0,38

1,6313

0,2969

0,76

1,8756

0,3413

-0,37

1,1492

0,2092

0,01

1,3935

0,2536

0,39

1,6377

0,2981

0,77

1,8820

0,3425

-0,36

1,1557

0,2103

0,02

1,3999

0,2548

0,40

1,6442

0,2992

0,78

1,8884

0,3436

-0,35

1,1621

0,2115

0,03

1,4063

0,2559

0,41

1,6506

0,3004

0,79

1,8948

0,3448

-0,34

1,1685

0,2127

0,04

1,4128

0,2571

0,42

1,6570

0,3016

0,80

1,9013

0,3460

-0,33

1,1749

0,2138

0,05

1,4192

0,2583

0,43

1,6635

0,3027

0,81

1,9077

0,3472

-0,32

1,1814

0,2150

0,06

1,4256

0,2594

0,44

1,6699

0,3039

0,82

1,9141

0,3483

-0,31

1,1878

0,2162

0,07

1,4320

0,2606

0,45

1,6763

0,3051

0,83

1,9206

0,3495

-0,30

1,1942

0,2174

0,08

1,4385

0,2618

0,46

1,6827

0,3062

0,84

1,9270

0,3507

-0,29

1,2007

0,2185

0,09

1,4449

0,2630

0,47

1,6892

0,3074

0,85

1,9334

0,3518

-0,28

1,2071

0,2197

0,10

1,4513

0,2641

0,48

1,6956

0,3086

0,86

1,9398

0,3530

-0,27

1,2135

0,2209

0,11

1,4578

0,2653

0,49

1,7020

0,3098

0,87

1,9463

0,3542

-0,26

1,2199

0,2220

0,12

1,4642

0,2665

0,50

1,7084

0,3109

0,88

1,9527

0,3554

-0,25

1,2264

0,2232

0,13

1,4706

0,2676

0,51

1,7149

0,3121

0,89

1,9591

0,3565

-0,24

1,2328

0,2244

0,14

1,4770

0,2688

0,52

1,7213

0,3132

0,90

1,9655

0,3577

-0,23

1,2392

0,2255

0,15

1,4835

0,2700

0,53

1,7277

0,3144

0,91

1,9720

0,3589

-0,22

1,2457

0,2267

0,16

1,4899

0,2711

0,54

1,7341

0,3156

0,92

1,9784

0,3600

-0,21

1,2521

0,2279

0,17

1,4963

0,2723

0,55

1,7406

0,3168

0,93

1,9848

0,3612

-0,20

1,2585

0,2291

0,18

1,5028

0,2735

0,56

1,7470

0,3179

0,94

1,9913

0,3624

-0,19

1,2649

0,2302

0,19

1,5092

0,2747

0,57

1,7534

0,3191

0,95

1,9977

0,3635

-0,18

1,2714

0,2314

0,20

1,5156

0,2758

0,58

1,7599

0,3203

0,96

2,0041

0,3647

-0,17

1,2778

0,2326

0,21

1,5220

0,2770

0,59

1,7663

0,3214

0,97

2,0105

0,3659

-0,16

1,2842

0,2337

0,22

1,5285

0,2782

0,60

1,7727

0,3226

0,98

2,0170

0,3671

-0,15

1,2906

0,2349

0,23

1,5349

0,2793

0,61

1,7791

0,3238

0,99

2,0234

0,3682

-0,14

1,2971

0,2361

0,24

1,5413

0,2805

0,62

1,7856

0,3249

1,00

2,0298

0,3694

-0,13

1,3035

0,2372

0,25

1,5477

0,2817

0,63

1,7920

0,3261

 

 

 

12. Значения постоянной хорды  ŝc  для колес без смещения

mn, мм 1 1,25 1,5 2 2,5 3 3,5
ŝc 1,387 1,734 2,081 2,774 3,468 4,161 4,855
ĥ*с 0,748 0,935 1,121 1,495 1,869 2,243 2,617
mn, мм 4 5 6 7 8 9 10
ŝc 5,548 6,935 8,323 9,710 11,097 12,484 13,871
ĥ*с 2,990 3,738 4,486 5,223 5,891 6,728 7,476

 Табличные данные определены по формулам: для постоянной хорды ŝc=1,387mn,
  для высоты до постоянной хорды ĥ*с=0,748mn

13. Значение коэффициента К (α= 20°) К = invαt /  invα
 

ß

К

ß

К

 ß

К

 ß

К

8°00'

1,0283

16°00'

1,1192

24°00'

1,2933

32°00'

1,5952

8 10

1,0295

16 10

1,1219

24 10

1,2980

32 10

1,6033

8 20

1,0308

16 20

1,1246

24 20

1,3029

32 20

1,6116

8 30

1,0321

16 30

1,1274

24 30

1,3078

32 30

1,6200

8 40

1,0334

16 40

1,1302

24 40

1,3127

32 40

1,6285

8 50

1,0347

16 50

1,1330

24 50

1,3177

32 50

1,6371

9 00

1,0360

17 00

1,1358

25 00

1,3227

33 00

1,6457

9 10

1,0374

17 10

1,1387

25 10

1,3278

33 10

1,6545

9 20

1,0388

17 20

1,1416

25 20

1,3330

33 20

1,6634

9 30

1,0402

17 30

1,1446

25 30

1,3382

33 30

1,6723

9 40

1,0417

17 40

1,1476

25 40

1,3435

33 40

1,6814

9 50

1,0432

17 50

1,1507

25 50

1,3488

33 50

1,6906

10 00

1,0447

18 00

1,1538

26 00

1,3542

34 00

1,6999

10 10

1,0462

18 10

1,1569

26 10

1,3597

34 10

1,7092

10 20

1,0478

18 20

1,1600

26 20

1,3652

34 20

1,7188

10 30

1,0494

18 30

1,1632

26 30

1,3708

34 30

1,7284

10 40

1,0510

18 40

1,1664

26 40

1,3765

34 40

1,7381

10 50

1,0527

18 50

1,1697

26 50

1,3822

34 50

1,7479

11 00

1,0544

19 00

1,1730

27 00

1,3880

35 00

1,7579

11 10

1,0561

19 10

1,1764

27 10

1,3938

35 10

1,7680

11 20

1,0578

19 20

1,1798

27 20

1,3997

35 20

1,7782

11 30

1,0596

19 30

1,1832

27 30

1,4057

35 30

1,7884

11 40

1,0614

19 40

1,1867

27 40

1,4117

35 40

1,7989

11 50

1,0632

19 50

1,1902

27 50

1,4178

35 50

1,8095

12 00

1,0651

20 00

1,1938

28 00

1,4240

36 00

1,8201

12 10

1,0670

20 10

1,1974

28 10

1,4303

36 10

1,8309

12 20

1,0689

20 20

1,2010

28 20

1,4366

36 20

1,8419



Вернуться наверх