Мощность и КПД. Цепные передачи обеспечивают передачу мощности в широком диапазоне — от долей до 5000 кВт (высокоскоростные передачи с параллельными контурами многорядных цепей). В передачах общего назначения мощность редко достигает 25-50 кВт.
Мощность (кВт) цепной передачи
![]()
где F — передаваемая окружная сила, Н; v — скорость цепи; ŋ— КПД передачи.
КПД цепной передачи зависит от силы, передаваемой цепью, и способа смазывания.
Для передач, работающих с номинальной нагрузкой (F > 0,1 QB где QB — разрушающая нагрузка цепи), ŋ= 0,95÷0,97 — при постоянном обильном смазывании (масляная ванна, 1 циркуляционное смазывание, масляный туман); ŋ = 0,92÷0,94 — при нерегулярном периодическом смазывании; ŋ = 0,9÷0,92 — при работе без смазки.
Натяжение цепи, динамические нагрузки и давление на опоры. Расчетная сила натяжения (Н) ведущей ветви цепи
Fp=F + F1 + Fдин , (2)
где F— полезная (окружная) сила, передаваемая цепью, Н; F1 =Fo+Fu— сила натяжения ведомой ветви цепи;
Fo— сила натяжения от собственной силы тяжести холостой ветви; Fu — сила натяжения от действия центробежных сил; Fдин — динамическая нагрузка.
При известной передаваемой мощности
![]()
Натяжение от силы тяжести (Н) при горизонтальном (и близком к нему) положении линии, соединяющей оси звездочек,
![]()
где m — масса 1 м цепи, кг; g= 9,81 м/с2 — ускорение свободного падения; a — межосевое расстояние, м;
f — стрела провисания ветви.
При вертикальном (и близком к нему) положении линии центров звездочек
F0 = mga . (5)
Натяжение цепи от действия центробежных сил
Fц=mv2 . (6)
Расчетная динамическая нагрузка, обусловленная неравномерностью движения,
![]()
где F 'дин = λn21J / 90 — динамическая нагрузка от неравномерности движения ведомой звездочки и приведенных к ней масс;
F ''дин = m1n21t /180 — динамическая нагрузка от неравномерности движения цепи;
λ= π / z2 — коэффициент, учитывающий влияние числа зубьев ведомой звездочки;
n1— частота вращения ведущей звездочки;
J — момент инерции ведомой звездочки и всех сопряженных вращающихся деталей на ее валу;
m1 = am— масса ведущей ветви;
t — шаг цепи;
∆y — коэффициент, учитывающий влияние упругости и провисания цепи
(∆y=0,5 при a=30t ; ∆y=0,75 при а=80t).
Центробежная сила на валы и опоры не передается. Нагрузку на них от полезного натяжения и собственной силы тяжести цепи условно принимают равной 1,15 F для горизонтальных передач и 1,05 F — для вертикальных.
Скоростные параметры передачи и выбор шага цепи. Скорость цепи и частоты вращения звездочек ограничиваются износом и прочностью тонкостенных деталей шарниров цепи. С увеличением скорости возрастает суммарный путь трения в единицу времени, а также сила удара шарниров цепи о зубья звездочек, усиливается шум передачи.
Допускаемая скорость цепи зависит от многих факторов, в наибольшей степени от точности цепи, шага ее звеньев, числа зубьев z1 ведущей звездочки, способа смазки.
Скорость цепи обычно принимают не более 15 м/с. При особо благоприятных условиях (высокая точность, малый шаг, большое число зубьев ведущей звездочки, небольшая нагрузка) скорость цепи может достигать 30—35 м/с.
При конструировании передач задают частоту вращения ведущей звездочки, n1 и выбирают число зубьев малой (обычно ведущей) звездочки, после чего, руководствуясь известными зависимостями предельно допустимой частоты вращения от числа зубьев звездочки и шага цепи (рис. 1, табл. 52), выбирают значение последнего. По этим трем параметрам вычисляют скорость цепи (м/с)
![]()
где z1 — число зубьев малой (ведущей) звездочки; n1 — частота ее вращения, мин-1.
По найденному значению скорости и шагу цепи выбирают способ смазки цепи (табл. 53).
Передаточное отношение и неравномерность вращения ведомой звездочки. При постоянной угловой скорости вращения ведущей звездочки w1 скорость цепи υ, угловая скорость вращения ведомой звездочки w2 и передаточное отношение u = w1/ w2 не остаются постоянными. Это обстоятельство учитывают при расчете передач, к которым предъявляют требования по кинематической точности вращения ведомого вала.
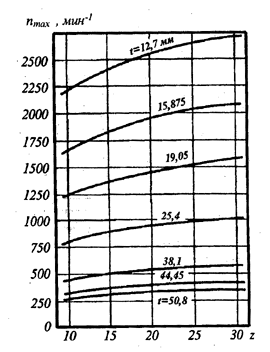
Рис. 1. Зависимости предельно допустимой
частоты вращения звездочки от числа
ее зубьев и шага цепи
При допущении прямолинейности ведущей ветви цепи (рис .2) скорость цепи
u=w1Rcosa,
где а — текущий угол поворота ведущей звездочки относительно перпендикуляра к ведущей ветви.
Так как угол а изменяется в пределах 0 — π/z1, то скорость u при повороте на один угловой шаг колеблется в пределах от umax= w1R1 до umin= w1R1 cos(π/z1).
52. Наибольшие рекомендуемые nр и предельные nпр частоты вращения
малой звездочки передач с роликовыми и втулочными цепями
| Частота вращения, мин-1 |
Шаг цепи, мм | |||||||||||
| 8 | 9,52 | 12,7 | 15,875 | 19,05 | 25,4 | 31,75 | 38,1 | 44,45 | 50,8 | 63,5 | 78,1 | |
| nр | 3000 | 2500 | 1250 | 100 | 900 | 800 | 630 | 500 | 400 | 300 | 200 | 150 |
| nпр | 6000 | 5000 | 3100 | 2300 | 1800 | 1200 | 1000 | 900 | 600 | 450 | 300 | 210 |
|
Примечания:1. При частоте вращения nр число зубьев малой звездочки должно быть |
||||||||||||
53. Способы смазывания цепных передач
| Параметры передачи | Смазка | |
| Скорость цепи v, м/с | Шаг цепи t, мм | |
| 1,5 1,0 0,5 |
19,05 25,4-38,1 44,45-50,8 |
Ручная через 8-10ч |
| 1 | 38,1-50,8 | Внутришарнирная |
| 4 3 1,6 |
15,875 19,05-31,75 38,1-50,8 |
Капельная |
| 8 6 4 |
15,875 19,05-31,75 38,1-50,8 |
Масляная ванна |
| 12 10 7 |
15,875 19,05-31,75 38,1-50,8 |
Струйная |
| 15 12 8 |
15,875 19,05-31,75 38,1-50,8 |
Разбрызгиванием |
| 12 8 |
31,75 38,1-50,8 |
Распылением (масляный туман) |
Мгновенная угловая скорость ведомой звездочки
![]()
где угол ß меняется в пределах от 0 до π/z2
![]()
Коэффициент неравномерности вращения ведомой звездочки при равномерном вращении ведущей звездочки
![]()
Среднее передаточное число из условия равенства средней скорости цепи на звездочках z1n1t= z2 n2 t
![]()
Максимальное значение передаточного числа ограничивается дугой обхвата цепью малой (ведущей) звездочки и числом шарниров, находящихся на этой дуге. Рекомендуется угол обхвата принимать не менее 120°, а число шарниров на дуге обхвата — не менее пяти-шести. Это условие выполняется при любых межосевых расстояниях а, если u < 3,5, а при u > 7 величина авыходит за пределы оптимальных. Поэтому обычно принимают u ≤ 6 и лишь в исключительных случаях u = 7 ... 10.

Рис. 2. Кинематическая схема цепной передачи (a) и график скорости цепи (б)
Параметры исходного цепного контура. Предпочтительны двухзвездные передачи с горизонтальным или близким к нему расположением линии, соединяющей оси звездочек. Рекомендуется избегать вертикального расположения ведомой ветви, так как при этом уменьшается ее натяжение от силы тяжести [см. (4) и (5)] и ухудшается зацепление.
Ведущей может быть как верхняя, так и нижняя ветвь. Однако в передачах с малым расстоянием между осями звездочек (а < 30t при u > 2, во избежание захлестывания ведомой ветви, а также в горизонтальных передачах с а > 60t и малым числом зубьев звездочек, во избежание соприкосновения ветвей, ведущей должна быть верхняя ветвь. При малых расстояниях между цепью и стенками картера, наоборот, ведущей целесообразно делать нижнюю ветвь.
Число зубьев звездочек. С уменьшением числа зубьев возрастают нагрузки в шарнирах и путь трения при их повороте, увеличивается неравномерность движения и скорость удара шарниров о зубья звездочек, снижается долговечность передачи, усиливается шум. Поэтому предельно допустимые минимальные значения чисел зубьев zmin=7 нежелательны даже для тихоходных и малонагруженных передач.
Для силовых передач общего назначения минимальное число зубьев
z1=zmin= 29-2u≥13. (14)
Для обеспечения равномерного износа зубьев звездочки и самой цепи при обычно принимаемом четном числе звеньев в контуре значение z1, вычисляемое по этой зависимости, округляют до ближайшего большего из ряда: 13, 15, 17, 21, 23, 25; при этом предпочтение отдают простым числам (13, 17, 23 и т.д.).
Для высокоскоростных передач с v > 20 м/с принимают zmin ≥ 35. Максимальное число зубьев большой (обычно ведомой) звездочки может достигать z2= 120 и более. Максимальное число зубьев звездочки лимитирует предельно допустимое увеличение шага цепи по зацеплению ∆y %. При заданном значении ∆y % наибольшее число зубьев большой (обычно ведомой) звездочки
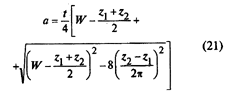
где D — диаметр ролика цепи (для втулочных цепей — диаметр втулки).
Расстояние между осями (центрами) звездочек. Минимальное расстояние между осями звездочек, мм: при u ≤ 3
amin= R1е+ R2е+(30...50); (16)
при u > 3 (из условия обеспечения угла обхвата цепью малой звездочки ≥ 120°)
.gif)
Оптимальное межосевое расстояние
а = (30 ... 50) t. (18)
Значение а рекомендуется принимать в пределах
amin ≤ а < 80t (19)
Число звеньев в контуре двухзвездной передачи
.gif)
где a0 — предварительно выбранное расстояние между осями звездочек.
Значение, вычисленное по (20), округляют до ближайшего большего четного числа W, имеющего с числами зубьев звездочек z1 и z2 меньшие общие делители (например, 2). Четное число звеньев в контуре позволяет избежать применения переходных звеньев. После уточнения числа звеньев в контуре уточняют требуемое расстояние между центрами звездочек:
.gif)
и определяют длину контура W t.
Дополнительные источники
1. Готовцев А.А., Котенок И.П. Проектирование цепных передач. Справочник. М.: Машиностроение, 1982.
2. Справочник по расчету и конструированию втулочных и втулочно-роликовых цепных передач / Г.А. Романовский, М.В. Окунев, М. Б. Блонский и др. М.: Машиностроение, 1966.
3. Машиностроение. Энциклопедия в 40 томах. Т. IV-1. Детали машин. Конструкционная прочность. Трение, износ, смазка. Под ред. Решетова Д.Н. М.: Машиностроение, 1