ШВП с натягом

Для передачи с натягом эквивалентную нагрузку находят с учетом силы F_нат предварительного натяга [1].

ШВП с натягом состоит из двух гаек, каждая из которых после сборки нагружена осевой силой F_нат натяга. Внешняя осевая сила F изменяет силы, действующие на гайки, нагружая одну гайку (рабочую) и разгружая другую (нерабочую). Как показали исследования [4], при достижении силой
F значений, в ~2,83 раза превышающих силы F_нат натяга, происходит полная разгрузка нерабочей гайки и всю внешнюю осевую силу воспринимает рабочая гайка.
В зависимости от направления внешней осевой силы F рабочей может быть как одна (левая), так и другая (правая) гайка.
Циклограмма нагружения представлена общим Числом г уровней нагружения. Из них j уровней нагружения с осевыми силами F_лi, положительного направления, за которое принято направление действия осевой силы на передачу со стороны левой гайки.
При этом сила Q_i, нагружающая на каждом уровне (i от 1 до j):
- левую (рабочую) гайку
                    Q_лi = F_нат ( 1 + 0,25 F_лi /F_нат  )²;
- правую (нерабочую) гайку
                     Q_пi = Q_лi  ^- F_лi . 
Циклограмма нагружения представлена числом (r - j) уровней нагружения с осевыми силами F_пi отрицательного направления, за которое принято направление действия осевой силы на передачу со стороны правой гайки.
При этом сила Q_i, нагружающая на каждом уровне [i от (j +1) до r):
- правую (рабочую) гайку
                   Q_пi = F_нат ( 1 - 0,25 F_пi /F_нат  )²;
- левую (нерабочую) гайку  
                    Q_лi = Q_пi + F_пi .
В приведенных формулах силы F_лi, и F_пi подставляют со своими знаками:
силыF_лi - со знаком плюс;
силы F_пi  - с0 знаком минус.
Средняя частота вращения при задании времени t_i , работы на каждом уровне в %:
                                           (8)
  Эквивалентная нагрузка для расчета ресурса левой гайки
                
  Эквивалентная нагрузка для расчета ресурса правой гайки:
               
  При расчете на ресурс ШВП с натягом принимают в качестве эквивалентной нагрузки F_E наибольшую из Q_лЕ и Q_пЕ :
               F_E =  Q_лЕ или Q_пЕ                           (9)

  При расчете на статическую грузоподъемность ШВП с натягом расчетной силой F_p служит наибольшая из двух
              F_E =  Q_лi max или Q_пi max   ^,          (10) 
  гле Q_лi max (или Q_пi max) - наибольшая из общего числа r уровней нагружения с учетом преднатяга сила, действующая на левую (или правую) гайку передачи.
  Растет на статическую прочность. Статическая прочность поверхности качения обеспечена, если расчетная осевая сила F_p [см. (7), (10)] не превосходит скорректированную статическую грузоподъемность С_0ар [см.(З)]:
           F_p ≤ С_0ар.
  Расчет передачи на заданный ресурс.
  Фактический ресурс L_hф передачи в ч:
              L_hф = 10⁶(C_ap/F_Е)³ /(60n_ср),
где С_ар - скорректированная динамическая грузоподъемность, Н [см. (3)];
 F_E  - эквивалентная нагрузка, Н [см. (5), (9)];
 n_ср  - средняя частота вращения, мин^-1.
  Передача пригодна, если  L_hф ≥  L_h , где  L_h - заданный ресурс. При невыполнении этого условия следует перейти на типоразмер передачи с большей динамической грузоподъемностью.

Проверка винта на статическую устойчивость. Винты передачи подвержены воздействию значительной осевой силы. В зависимости от схемы осевой фиксации вращающиеся винты работают на растяжение или сжатие.
  Вычисляют значение критической силы F_KP ,  Н, по Эйлеру:

               F_кр = π³ Ed⁴ / [64S(μl)²],

  где Е - модуль упругости материала винта, МПа (для стали E=2,1·10⁵ МПа); d - диаметр резьбы винта по впадинам, мм; для предварительных расчетов можно принимать, d = d_o - D_w, S -коэффициент запаса, S =1,5÷4 (обычно S =3); μ- коэффициент, зависящий от способа закрепления винта (табл. 19); l - длина нагруженного (неопорного) участка винта, мм.
  Статическая устойчивость обеспечена, если 
           F_max ≤  F_кр,
 где F_max - наибольшая осевая сила (Н), нагружающая винт на длине l [см. (1)].
  В ОСТ 2 Н62-6-85 приведены номограммы для выбора типоразмера ШВП по допустимой величине осевой силы для различных схем монтажа.

19. Значения коэффициентов  μ и v

  Примечание. Принятые условные обозначения: - заделка; - шарнир.
  Проверка на динамическую устойчивость. В соответствии с ОСТ 2 РЗ1-5-89 предельную частоту n_пред вращения ШВП регламентируют двумя факторами: критической частотой n_кр, вращения и линейной скоростью движения шарика, последнюю в свою очередь ограничивают фактором
      d₀n ≤ 8·10⁴, мм·мин^-1.
  В технически обоснованных случаях допускают  d₀n ≤ 12·10⁴, мм·мин^-1.
  Критическую частоту n_кр, мин^-1, вращения вычисляют из условия предотвращения резонанса:
      n_кр=5·10⁷vK_вd /l²,
  где v - коэффициент, зависящий от способа закрепления винта (табл. 19); К_в - коэффициент запаса по частоте вращения, К_в =0,5÷0,8; d и l - 
  в мм.
  В качестве предельной частоты n_пред , мин^-1, вращения принимают наименьшую из n_пред=n_кр и  n_пред=8•10⁴/d₀.
  Частота вращения находится в допустимых пределах при выполнении условия
    n_max ≤ n_пред ,
 где n_max- наибольшая частота вращения, мин^-1 [см. (2)].

  Определение КПД. Коэффициент полезного действия шариковинтовой передачи, преобразующей вращательное движение в поступательное:
  при ведущем винте

  при ведущей гайке

  где ψ - угол подъема резьбы, рад:

  К_нат - коэффициент, учитывающий влияние натяга; р - приведенный угол трения в резьбе, рад:

р = arctg[f_k / (0,5D_w sin a)].

  Здесь f_к - коэффициент трения качения, мм (f_к =0,005...0,015 мм); а - угол контакта, а=45°=0,785 рад.
  Коэффициент К_нат = 1 для передач без натяга (с зазором) и для передачи с небольшим натягом: 
  при F_нат ≤ F_mаx  /3 . Силу F_нат устанавливают из расчета жесткости передачи, см. (4); F_mаx  - см- (1).
  Для передачи со значительным натягом (При F_нат >  F_mаx / 3 )

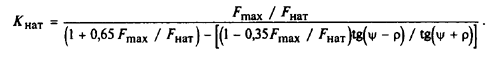
  Момент холостого хода для передачи с натягом, Н-м:

  где K_T - коэффициент, учитывающий влияние точности изготовления (табл. 16);
  F_нат - в Н; d_o - в мм.
  Наибольший момент завинчивания, Н-м: T_зав = 0,5•10^-3 F_mаx zP/ ( πη ) + T_xx , где Р - шаг резьбы, мм; z - число заходов резьбы; F_mаx - в Н [см. (1)].
  Наибольшая линейная скорость v, м/с, перемещения ведомого элемента вычисляют в зависимости от частоты вращения n_max , мин^-1 [см. (2)]:

v = Рzn_max / 60000.

  Расчет геометрии профиля резьбы. Радиус шарика, мм: r_w = D_w / 2.
  Радиус профиля резьбы, мм (рис. З):

r_пр =(1,03...1,05)r_w.

  Число шариков в одном витке гайки:

z_ш =πd_o/(D_wcos_ψ) .

  Число рабочих шариков в одном витке с вкладышем: z_p =z_ш - z', где z' - число шариков в канале возврата, 
z' = ЗР / D_w,. 
  Расчетное число шариков в i_в витках:

z_pacч=0,7z_pi_B.

  Нормальная сила, нагружающая один шарик, Н: F_n = F_p / (z_pacч sin a cos_ψ ) ,  
  где F_p - расчетная сила, Н [см. (7), (10)].
  Параметры площадки контакта между телом качения и дорожкой качения (здесь Е - модуль упругости, МПа):

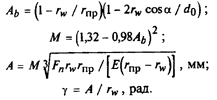
   Радиус галтели винта, мм: r_B≈ 0,2 r_W .
   Радиус галтели гайки, мм: r_Г≈ 0,15 r_W .
   Наружный диаметр резьбы винта, мм:

d₁ = d₀ - 2[(r_W + r_B)cos(a + у) - r_B]. 

  Смещение центра радиуса профиля, мм:

с_пр=(r_пр- r_W)sina.

  Внутренний диаметр резьбы винта, мм:

d_2B =d₀ + 2c_пр - 2r_пр .

  Наружный диаметр резьбы гайки, мм: 

d_2r =d₀ - 2c_пр + 2r_пр .

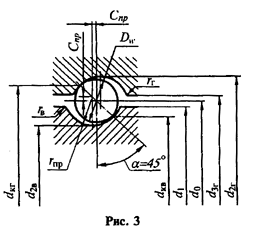
  Внутренний диаметр резьбы гайки, мм:

d_3r =d₀ +0,5(d₀-d₁).

   Диаметр качения по винту, мм:

d_кв =d₀-2r_Wcosa .

  Диаметр качения по гайке, мм:

d_кг =d₀+2r_Wcosa .

  Расчет стержня винта на прочность. Напряжения σ, МПа, растяжения-сжатия при нагружении силой
  F_mаx , Н [см. (1)]:

  Напряжения τ, МПа, кручения при нагружении наибольшим моментом T_зав, Н-м, завинчивания:
  τ = 10³T_зав /(0,2d³_2B).
  Прочность винта проверяют по эквивалентному напряжению, МПа:

  Допускаемое напряжение [σ] = σ_т / 3 , где σ_т - предел текучести материала винта, МПа.
  Осевая жесткость С_в, Н/мкм, винта диаметром d_кв, мм, и длиной l , мм, при закреплении:
  по схемам 1-3 (табл. 19)

  по схеме 4 (табл. 19)

  где Е - модуль упругости материала винта, МПа.
  Смещение гаек для создания предварительного натяга, мкм:

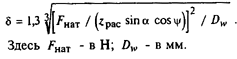
  Здесь F_нат - в Н; D_w - в мм.