Зубчатые передачи (Новикова, конические, червячные)

Краткое содержание: Зубчатые передачи с зацеплением М.Л.Новикова.Конические зубчатые передачи.Червячные зубчатые передачи.Зубчатые передачи с циклоидальными профилями.


Зубчатые передачи с зацеплением М.Л.Новикова.

С целью повышения несущей способности зубчатых передач М.Л.Новиков [1] разработал новый способ образования сопряженных поверхностей для различных видов зубчатых передач с параллельными, пересекающимися и перекрещивающимися осями. До Новикова исходили из того, что в передачах с параллельными осями поверхности зубьев находятся в линейном контакте, а их торцевые профили являются взаимоогибаемыми кривыми. Новиков предложил перейти от линейного контакта поверхностей к точечному. При этом профили зубьев в торцевом сечении могут быть не взаимоогибаемыми кривыми и их можно выполнять как выпуклый и вогнутый профили с малой разностью кривизн. В передаче с параллельными осями линия зацепления является прямой линией параллельной осям колес. Зацепление Новикова имеет только осевое перекрытие :где b - ширина зубчатого венца, pz - осевой шаг. Поэтому поверхности зубьев выполняются винтовыми (косозубыми) с углом подъема винтовой линии 

Одним из основных параметров зацепления Новикова является расстояние от полюса зацепления Р до точки контакта К, которое определяет положение линии зацепления ( прямой К-К параллельной осям вращения и проходящей через точку контакта К ) относительно оси мгновенного относительного вращения Р-Р. Согласно рекомендациям работы [ 14.1 ], это расстояние выбирается в зависимости от величины передаваемой мощности в пределах

Радиусы кривизны рабочих участков профилей рекомендуется выбирать для выпуклой поверхности ,для вогнутой поверхности , где k2 = 0.03 ... 0.1 .

Радиус окружности вершин колеса с выпуклыми зубьями:

где 

Дуги рабочих профилей выпуклых зубьев проводят от начальной окружности до окружности вершин. Радиус окружности вершин колеса с вогнутыми зубьями .

 где - глубина захода зубьев.

Радиус окружности впадин колеса с выпуклыми зубьями:

где c - радиальный зазор, приблизительно равный 

Радиус окружности впадин колеса с вогнутыми зубьями :

где  - межосевое расстояние в передаче .

Преимущества зубчатых передач с зацеплением Новикова:

  • повышенная контактная прочность зубьев, за счет использования зацепления вогнутого профиля с выпуклым ( приведенный радиус кривизны определяется суммой радиусов кривизны профилей );
  • перекрытие в передачах Новикова обеспечивается только за счет осевого перекрытия, поэтому высота зубьев может быть достаточно малой, что обеспечивает высокую изгибную прочность зубьев ( в целом, по приблизительным оценкам, нагрузочная способность передач Новикова в 2-3 раза выше, чем косозубых эвольвентных передач с одинаковыми размерами);
  • точечное зацепление (пятиподвижная кинематическая пара) обеспечивает в передачах с зацеплением Новикова меньшую чувствительность к монтажным погрешностям.

К недостаткам передач Новикова можно отнести

  • более сложную технологию изготовления, за счет использования инструмента с профилями криволинейной конфигурации;
  • наличие значительных осевых нагрузок на подшипники из-за использования винтовых зубьев с большими углами подъема винтовой линии;
  • склонность зубьев винтовых колес к излому у торца при входе в зацепление

Конические зубчатые передачи.

Конической называется зубчатая передача, предназначенная для передачи и преобразования вращательного движения между звеньями, оси вращения которых пересекаются.

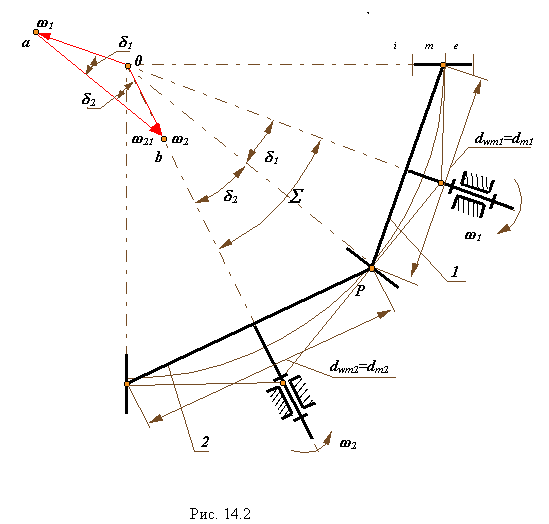
Схема конической передачи представлена на рис. 14.2. Оси колес зубчатой передачи пересекаются в точке 0. Угол S между осями колес ( или между векторами угловых скоростей звеньев w1 иw2 ) называется межосевым углом. Этот угол может изменяться в пределах 0° < S < 180°. При S= 0° передача превращается в цилиндрическую с внешним зацеплением, а при S= 180° - в цилиндрическую с внутренним зацеплением. Таким образом, коническая передача является общим случаем зубчатой передачи, нежели цилиндрические. Начальные или аксоидные поверхности в конической передаче имеют форму конусов. Аксоидными называются поверхности, которые образуются осями мгновенного относительного вращения колес, в системах координат связанных с колесами ( звеньями передачи ). Если колеса передачи обработаны без смещения исходного контура, то аксоидные поверхности совпадают с делительными. При относительном движении аксоиды перекатываются друг по другу, при этом скольжение возможно только в направлении оси относительного вращения. Поэтому вектора угловых скоростей звеньев связаны между собой векторным уравнением

если известна величина w1, то из этого уравнения можно определить w1 и w2. Из векторного треугольника D a0b

Передаточное отношение конической передачи

Так как тo 

Тогда углы начальных ( делительных при х=0 ) конусов

Геометрия зацепления в конической зубчатой передаче:

Как и в цилиндрических, так и в конических зубчатых передачах наиболее часто применяют эвольвентное зацепление. Эвольвентная поверхность зуба конического колеса образуется при перекатывании производящей плоскости по основному конусу. Эвольвентные кривые формируются на соосных сферических поверхностях с центром в вершине основного конуса. Поэтому для расчета геометрии эвольвентной конической передачи необходимо применять сферическую геометрию. Так как это сложно, то используют приближенный метод расчета геометрии - метод дополнительных конусов [2], предложенный английским столяром Томасом Тредгольдом. При этом методе расчет геометрии проводится для эквивалентного цилиндрического зацепления двух секторов. Эти сектора образуются развертками конусов, которые построены на внешней сфере радиуса R we . Радиусы оснований этих конусов r we1 = r e1 и r we2 = r e2 , а образующие являются касательными к сфере (рис.14.3). Числа зубьев колес эквивалентного цилиндрического зацепления рассчитываются на основании следующих формул

где rte1и rte2 - радиусы торцевых делительных окружностей на внешней сфере, rvte1и rvte2- радиусы делительных окружностей эквивалентного цилиндрического зацепления.

Так как то :

где z1 и z2 - числа зубьев колес конической передачи, zvt1 и zvt2 - числа зубьев колес эквивалентного цилиндрического расчетного зацепления ( эти величины могут быть дробными).

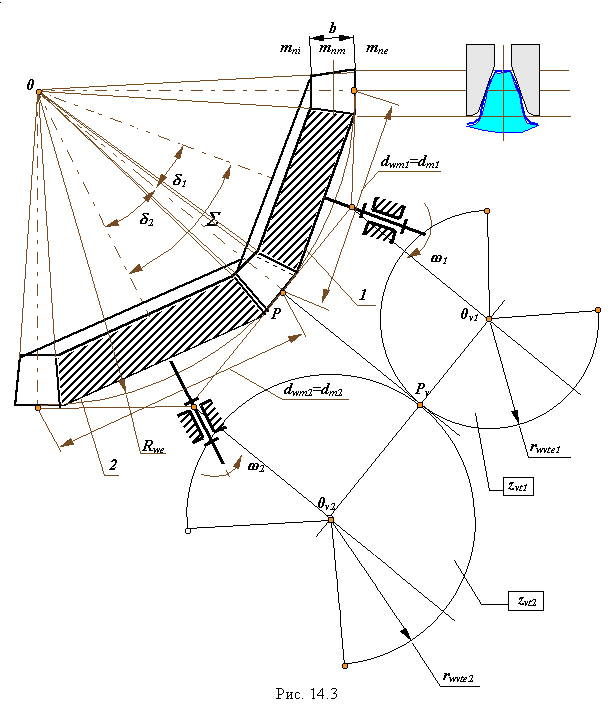
После определения чисел зубьев эквивалентного цилиндрического зацепления, приближенный расчет геометрических параметров для внешнего торца конического зацепления можно проводить по рассмотренным выше формулам цилиндрического эвольвентного зацепления. Радиус внешней сферы (длина образующей начального или делительного конуса)

Ширина зубчатого венца , где b=0.3....0.4 - коэффициент ширины зубчатого венца.

По форме линии зуба конические зубчатые передачи различаются на: прямозубые; косозубые; с круговым зубом; с эвольвентной линией зуба; с циклоидальной линией зуба

Преимущества и недостатки конических зубчатых передач.

Преимущества:

  • обеспечение возможности передачи и преобразования вращательного движения между звеньями с пересекающимися осями вращения;
  • возможность передачи движения между звеньями с переменным межосевым углом при широком диапазоне его изменения;
  • расширение компоновочных возможностей при разработке сложных зубчатых и комбинированных механизмов.

Недостатки:

  • более сложная технология изготовления и сборки конических зубчатых колес;
  • большие осевые и изгибные нагрузки на валы, особенно в связи с консольным расположением зубчатых колес.

Червячные зубчатые передачи.

Червячной - называется зубчатая передача, состоящая из двух подвижных звеньев - червяка и зубчатого колеса и предназначенная для передачи и преобразования вращательного движения между ортагональными перекрещивающимися осями. Червяком называют звено, наружная поверхность которого имеет форму винта. Червячным колесом называется зубчатое колесо с косыми зубьями, которое зацепляется с червяком

Виды червячных передач и червяков ( по ГОСТ 18498-73 ).

  1. по виду делительной поверхности червяка
    • цилиндрические червячные передачи - червяк и колесо в передаче имеют цилиндрические делительные и начальные поверхности;
    • глобоидные червячные передачи - делительная и начальная поверхности червяка образованы вращением отрезка дуги делительной или начальной поверхности парного червячного колеса вокруг оси червяка;
  2. по виду теоретического торцового профиля витка червяка
    • архимедов червяк (ZA) - профиль выполнен по архимедовой спирали;
    • эвольвентный червяк (ZI) - профиль выполнен по эвольвенте окружности;
    • конволютный червяк (ZN) - профиль выполнен по удлиненной эвольвенте

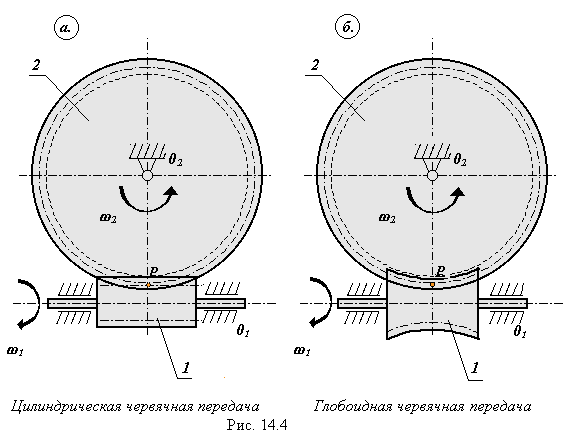
Геометрия зацепления цилиндрической червячной передачи

Расчет геометрии зацепления цилиндрической червячной передачи регламентируется ГОСТ 19650 - 74 [3]. Связь между основными параметрами червяка - диаметром начального цилиндра d w1, ходом винтовой линии pz1 и углом ее наклона bw - устанавливается следующим соотношением

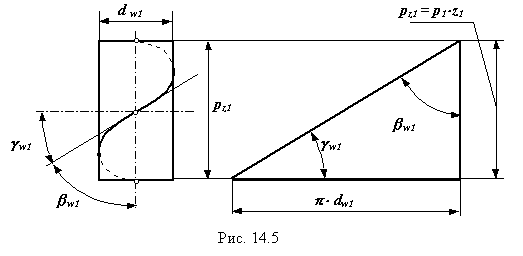
Связь между ходом винтовой линии pz1 и шагом многозаходного винта p1

Расчет геометрии зацепления.

Исходные данные:


m - модуль осевой;
q - коэффициент диаметра червяка;
z1 - число витков червяка;
aw - межосевое расстояние;
x - коэффициент смещения червяка;
u - передаточное число.

Параметры инструмента:


h* = (h*w + c*1) - коэффициент высоты витка;
h*a - коэффициент высоты головки;
s* - коэффициент расчетной толщины;
r*f - коэффициент радиуса кривизны переходной кривой;


c*1,2 = 0.25 ... 0.5 ; s* = 0.75 Ч p ; r*f = 0.3 ... 0.45 .

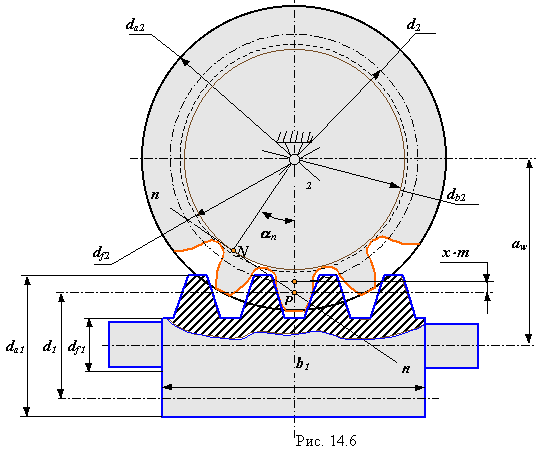
Расчет геометрических параметров.

  1. Число зубьев колеса 
  2. Коэффициент смещения ( если задано межосевое расстояние )

    • Межосевое расстояние ( если задан коэффициент смещения )

  3. Делительные диаметры

  4. Начальные диаметры

  5. Делительный угол подъема витка червяка

  6. Начальный угол подъема витка червяка

  7. Основной угол подъема витка червяка ( только для червяков ZI )

    и основной диаметр червяка 

  8. Высота витка червяка

  9. Высота головки витка червяка

  10. Диаметры вершин

    витков червяка 

    зубьев червячного колеса в средней торцовой плоскости 

     

  11. Диаметры впадин

    червяка 

    червячного колеса 

     

  12. Наибольший диаметр червячного колеса

  13. Ширина венца червячного колеса

  14. Длина нарезанной части червяка ( при х= 0 )

Геометрические показатели качества зацепления.

  1. Подрезание зубьев червячного колеса отсутствует если

  2. Заострение зубьев в средней торцовой плоскости отсутствует, если

  3. Заострение зубьев в средней торцовой плоскости отсутствует, если

Преимущества и недостатки червячных зубчатых передач

Преемущества:

  • благодаря малому числу заходов червяка (z1= 1...4) червячная передача позволяет реализовывать в одной ступени большие передаточные отношения;
  • обладает высокой плавностью, низким уровнем вибраций и шума;
  • позволяет обеспечить самоторможение червячного колеса ( при малых углах подъема витка передача движения от вала червячного колеса к червяку становится невозможной)

Недостатки:

  • высокая скорость скольжения вдоль линии зуба, что ведет к повышенной склонности к заеданию ( необходимы специальные смазки и материалы для зубчатого венца червячного колеса ), снижению КПД и более высокому тепловыделению .

Зубчатые передачи с циклоидальными профилями.

Циклоидальными кривыми или циклоидами (рулеттами, трохоидами) называется семейство кривых, которые описываются точками окружности или точками, связанными с этой окружностью, при ее перекатывании без скольжения по другой окружности или прямой [4]. Пусть образующая циклоиду точка лежит на окружности, тогда описываемая ей траектория будет эпициклоидой при внешнем контакте окружностей, гипоциклоидой - при внутреннем, или просто циклоидой - при перекатывании по прямой. Если образующая точка лежит вне окружности или внутри нее, то описываемые ей циклоидальные траектории называются эпитрахоидами (удлиненными или укороченными эпициклоидами) при внешнем контакте окружностей, гипотрохоидами (удлиненными или укороченными гипоциклоидами) - при внутреннем.

Теорема Камуса.

Теорема Камуса доказывает что профили выполненные по циклоидальным кривым будут при определенных условиях сопряженными и взаимоогибаемыми. Теорема Камуса. Кривые, описываемые какой-либо точкой жестко связанной с некоторой вспомогательной центроидой при перекатывании ее по центроидам, определяющим относительное движение рассматриваемых звеньев, будут взаимоогибаемыми в относительном движении этих звеньев.

Рассмотрим схему изображенную на рис. 14.7. На этой схеме: Ц1-Ц1 и Ц2-Ц2 - центроиды, определяющие движение звеньев 1 и 2; Ц3-Ц3 - вспомогательная центроида, с которой жестко связана кривая М-М; К1-К1 - огибающая к положениям М-М при перекатывании Ц3-Ц3 и Ц1-Ц1; К2-К2 - огибающая к положениям М-М при перекатывании Ц3-Ц3 и Ц2-Ц2; К1-К1 и К2-К2- взаимоигибаемые кривые в относительном движении звеньев 1 и 2; дуга РР1 = дуге РР2 = дуге РР3; М'Р3 - нормаль к М-М из точки Р3;

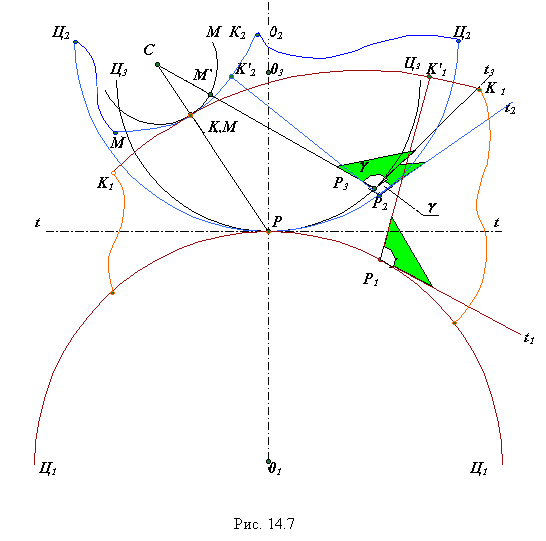
Через промежуток времени dt точки Р1, Р2 и Р3 совпадут Р, касательные и прямые М'P3, K'2P2 и K'1P1 сольются в одну, то есть точки K'2 и K'1 образуют контактную точку K, а прямые проходящие через нее и полюс Р (K'2P2 и K'1P1), согласно с требованиями теоремы Виллиса, образуют контактную нормаль. Рассмотрим схему зубчатой передачи с циклоидальным зацеплением, которая изображена на рис. 14.8. На этой схеме: rw1 и rw2 - радиусы начальных окружностей (центроид в относительном движении зубчатых колес), rv1 и rv2 - радиусы вспомогательных окружностей, точки которых образуют эпициклоиды Рa и гипоциклоиды Рb, используемые в качестве профилей при формировании зубьев.

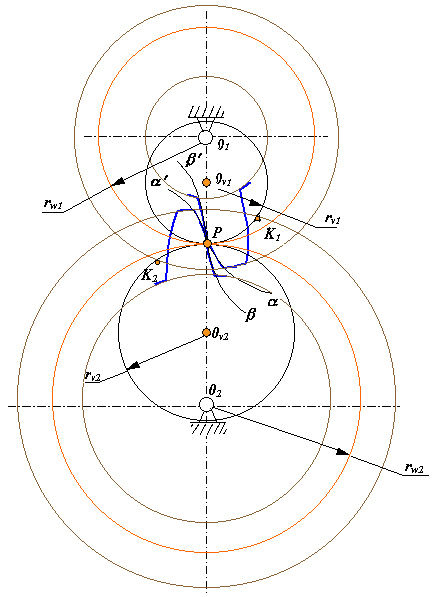
Рис. 14.8

Профиль головки зуба колеса 1 очерчен по эпициклоиде Рa , а профиль ножки по гипоциклоиде Рbў . На колесе 2 аналогично для профиля головки зуба используется эпициклоида Рaў , а для ножки - гипоциклоида Рb. Эпициклоиды Рa и Рaў получены при перекатывании вспомогательной окружности rv1 соответственно по начальным окружностям rw1 и rw2 . Гипоциклоиды Рb иРbў получены при перекатывании вспомогательной окружности rv2 соответственно по начальным окружностям rw1 и rw2 . Геометрическое место точек контакта профилей в неподвижной системе координат - линия зацепления K1K2, образуется отрезками дуг вспомогательных окружностей PK1 и PK2 . Коэффициент перекрытия ea = (PK1 + PK2)/pw , где pw - шаг по начальной окружности rw1 ( или rw2 ). Исходный производящий контур реечного инструмента, используемый для обработки циклоидальных зубчатых колес образован двумя дугами циклоидальных кривых. Для нарезания двух колес необходимо иметь два инструмента с одним исходным производящим контуром, которые конгруентны друг другу (как шаблон и контршаблон).

Преимущества и недостатки циклоидального зацепления

Преемущества:

  • меньший износ профилей за счет использования зацепления выпуклого профиля с вогнутым;
  • больший, чем в аналогичной эвольвентной передаче, коэффициент перекрытия;
  • возможность получения на шестерне (трибе) без подрезания меньшего числа зубьев, нежели в эвольвентных зубчатых передачах;
  • меньшая скорость скольжения профилей

Недостатки:

  • более сложный профиль режущего инструмента, а следовательно, и большая стоимость изготовления;
  • чувствительность к монтажным погрешностям межосевого расстояния (изменение межосевого расстояния изменяет передаточное отношение).

Примечание: К разновидностям циклоидальных зацеплений относятся часовое и цевочное. В часовом зацеплении радиус вспомогательной окружности выбирается равным половине радиуса соответствующей начальной окружности. Тогда гипоциклоиды, образующие ножки зубьев, вырождаются в прямые линии. В цевочном зацеплении радиус вспомогательной окружности цевочного колеса принимают равным радиусу начальной окружности этого колеса. Профиль зуба цевочного колеса - окружность, а профиль зуба второго колеса - эквидистанта к эпициклоиде.

Контрольные вопросы к лекции 14

 

1. Какие зубчатые передачи используются для передачи вращения между параллельными и пересекающимися осями?(стр.1)

2. Чем отличаются эвольвентные зубчатые передачи от передач с круговинтовым зацеплением Новикова?(стр.1)

3. Укажите достоинства и недостатки зубчатых передач Новикова (стр.2-3)

4. Для каких целей используются конические зубчатые передачи?(стр.3-4)

5. Каковы особенности геометрии конических колес и передач?(стр.4-5)

6. Укажите достоинства и недостатки конических зубчатых передач(стр.6)

7. Как определить углы вершин начальных конусов в конической передаче при известном передаточном отношении и межосевом угле? (стр.4)

8. Какие виды червячных передач используются в механизмах?(стр.6-7)

9. Какими особенностями кинематики червячных передач вызвано скольжение зубьев?(стр.8-10)




Вернуться наверх