К основным задачам механики манипуляторов можно отнести:
|
Эти задачи решаются на базе общих методов исследования структуры, геометрии, кинематики и динамики систем с пространственными многоподвижными механизмами. Каждая из рассматриваемых задач может быть сформулирована как прямая (задача анализа) или как обратная (задача синтеза). При определении функций положения механизма, в прямой задаче находят закон изменения абсолютных координат выходного звена по заданным законам изменения относительных или абсолютных координат звеньев. В обратной - по заданному закону движения схвата находят законы изменения координат звеньев, обычно, линейных или угловых перемещений в приводах. Решение обратной задачи или задачи синтеза более сложно, так как часто она имеет множество допустимых решений, из которых необходимо выбрать оптимальное. В обратной задаче кинематики по требуемому закону изменения скоростей и ускорений выходного звена определяются соответствующие законы изменения скоростей и ускорений в приводах манипулятора. Обратная задача динамики заключается в определении закона изменения управляющих сил и моментов в приводах, обеспечивающих заданный закон движения выходного звена.
Кинематический анализ механизма манипулятора.
Первая и основная задача кинематики - определение функции положения. Для пространственных механизмов наиболее эффективными методами решения этой задачи являются векторный метод и метод преобразования координат. При решении прямой задачи о положении схвата манипулятора обычно используют метод преобразования координат. Из множества методов преобразования координат [ 1, 2 ] , которые отличаются друг от друга правилами выбора осей локальных систем координат, для манипуляторов обычно используется метод Денавита и Хартенберга.
Опишем два вида матриц:
матрицы М, определяющие отношение между системами координат соседних звеньев;
матрицы Т, определяющие положение и ориентацию каждого звена механизма в неподвижной или базовой системе координат.
Воспользуемся однородными координатами трехмерного проективного пространства РR3, в которых движение евклидова пространства R3 можно представить линейным преобразованием
![]() где Мij - матрица 4x4 вида
где Мij - матрица 4x4 вида 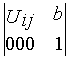 .
.
Это преобразование эквивалентно преобразованию в эвклидовом пространстве ![]() где
где ![]() . То есть преобразованию, которое включает поворот, определяемый матрицей Uij размерностью 3х3, и параллельный перенос, задаваемый вектором
. То есть преобразованию, которое включает поворот, определяемый матрицей Uij размерностью 3х3, и параллельный перенос, задаваемый вектором ![]() размерностью 3. В однородном пространстве положение точки будут определять не три x, y и z, а четыре величины x', y', z' и t', которые удовлетворяют следующим соотношениям:
размерностью 3. В однородном пространстве положение точки будут определять не три x, y и z, а четыре величины x', y', z' и t', которые удовлетворяют следующим соотношениям:
x = x'/t', y = y'/t', z = z'/t'.
Обычно принимают t'=1. У матрицы поворота Uij элементами uij являются направляющие косинусы углов между новой осью i и старой осью j. Вектор  - трехмерный вектор, определяющий положение начала новой системы координат i в старой системе j. Выбор расположения осей должен соответствовать решаемой задаче. При решении задачи о положениях необходимо: в прямой задаче определить положение выходного звена как функцию перемещений в приводах, в обратной - заданное положение выходного звена представить как функцию перемещений в приводах. Выбор расположения и ориентации локальных систем координат должен обеспечивать выполнение этих задач. При использовании метода Денавита и Хартенберга оси координат располагаются по следующим правилам:
- трехмерный вектор, определяющий положение начала новой системы координат i в старой системе j. Выбор расположения осей должен соответствовать решаемой задаче. При решении задачи о положениях необходимо: в прямой задаче определить положение выходного звена как функцию перемещений в приводах, в обратной - заданное положение выходного звена представить как функцию перемещений в приводах. Выбор расположения и ориентации локальных систем координат должен обеспечивать выполнение этих задач. При использовании метода Денавита и Хартенберга оси координат располагаются по следующим правилам:
1. Для звена i ось zi направляется по оси кинематической пары, образуемой им со звеном ( i+1). Начало координат размещают в геометрическом центре этой пары.
2. Ось xi направляется по общему перпендикуляру к осям zi-1 и zi с направлением от zi-1 к zi. Если оси zi-1 и zi совпадают, то xi перпендикулярна к ним и направлена произвольно. Если они пересекаются в центре кинематической пары, то начало координат располагается в точке пересечения, а ось xi направляется по правилу векторного произведения ![]() (кратчайший поворот оси zi до совмещения с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).
(кратчайший поворот оси zi до совмещения с zi-1 при наблюдении с конца xi должен происходить против часовой стрелки).
3. Ось yi направляется так, чтобы система координат была правой.
В прямой задаче необходимо определить положение схвата манипулятора и связанной с ним системы координат Mxnynzn по отношению к неподвижной или базовой системе координатKx0y0z0. Это осуществляется последовательными переходами из системы координат звена i в систему координат звена i-1. Согласно принятому методу, каждый переход включает в себя последовательность четырех движений: двух поворотов и двух параллельных переносов, осуществляемых в указанной последовательности (см. рис. 20.1):
 |
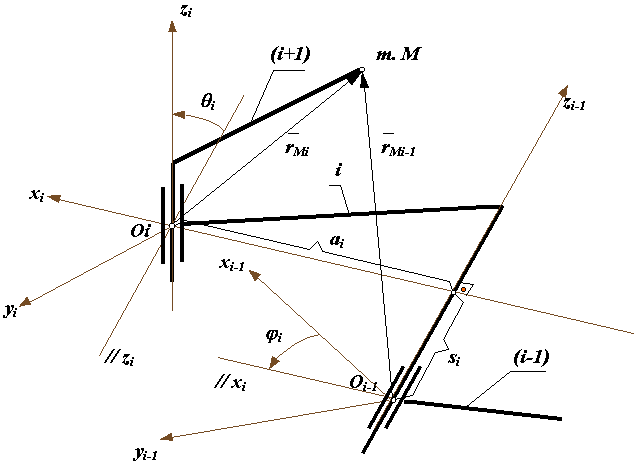 Рис. 20.1 |
Необходимо отметить, что знак угла поворота не имеет значения, так как в матрицах перехода используются направляющие косинусы (четные функции). Целесообразно рассматривать угол, обеспечивающий кратчайший поворот оси старой системы i до совмещения (параллельности) с соответствующей осью новой ( i-1). Перемещения начала координат определяются как координаты начала старой системы Oi в новой Oi-1.
В манипуляторах обычно используются одноподвижные кинематические пары или вращательные, или поступательные. Оба относительных движения как вращательное , так и поступательное, реализуются в цилиндрических парах. Поэтому при общем представлении механизма используются (рис.20.1) цилиндрические пары.
Матрицы перехода их системы Oi в систему Oi-1 можно записать так:
![]() ,
,
| где: | 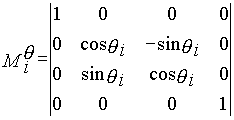 |
- матрица поворота вокруг оси xiна угол -qi, |
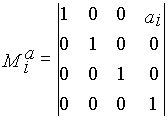 |
- матрица переноса вдоль оси xi на -ai, | |
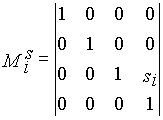 |
- матрица переноса вдоль оси zi-1 на -si, | |
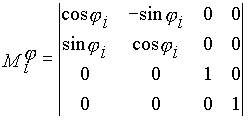 |
- матрица поворота вокруг оси zi-1 на угол -ji. |
В этих матрицах переменные si и ji соответствуют относительным перемещениям звеньев в кинематических парах и являются обобщенными координатами манипулятора, определяющими конфигурацию механизма в рассматриваемом положении. Переменные ai и qi определяются конструктивным исполнением звеньев манипулятора, в процессе движения они остаются неизменными.
Положение некоторой произвольной точки М в системе координат звена i определяется вектором rMi, а в системе координат звена (i-1) - вектором rMi-1. Эти радиусы связаны между собой через матрицу преобразования координат Мi следующим уравнением:
![]() ,
,
| где: | 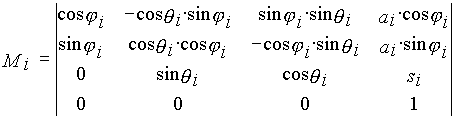 |
- матрица перехода из i-ой системы координат в (i - 1)-ю. |
Рассмотрим шестиподвижный манипулятор в исходном или начальном положении (рис.20.2). За начальное положение принимается такое, в котором все относительные обобщенные координаты равны нулю. Переход из системы координат любого i-го звена к неподвижной или базовой системе записывается в виде
![]() или
или ![]() ,
,
где 
![]() - матрица преобразования координат i-ой системы в координаты базовой системы координат.
- матрица преобразования координат i-ой системы в координаты базовой системы координат.
 |
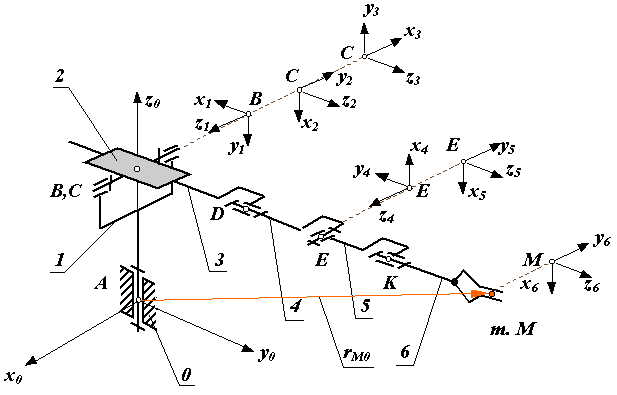 Рис. 20.2 |
Для схемы, изображенной на рис.20.2, радиус rM6 = 0, а радиус rM0 определится по формуле
![]() ,
,
то есть положение выходного звена манипулятора определяется матрицей Тn. Элементы этой матрицы определяют положение центра схвата точки М и ориентацию его в пространстве. Четвертый столбец определяет, декартовы координаты точки М (проекции вектора rM0на оси координат). Третий столбец содержит направляющие косинусы оси zn системы координат, связанной со схватом, или вектора подхода ![]() , который характеризует направление губок схвата (рис.20.3). Второй столбец определяет направление оси yn или вектора ориентации
, который характеризует направление губок схвата (рис.20.3). Второй столбец определяет направление оси yn или вектора ориентации ![]() , который проходит через центр схвата по оси перпендикулярной рабочим поверхностям его губок. В первом столбце содержатся направляющие косинусы оси xn или вектора
, который проходит через центр схвата по оси перпендикулярной рабочим поверхностям его губок. В первом столбце содержатся направляющие косинусы оси xn или вектора ![]() . Углом подхода схвата
. Углом подхода схвата ![]() называется угол между вектором подхода
называется угол между вектором подхода ![]() и базовым вектором
и базовым вектором
![]() ,
,
где ![]() - орт вектора
- орт вектора ![]() неподвижной или базовой системы координат. С учетом сказанного, матрица Tnможет быть представлена в следующем виде
неподвижной или базовой системы координат. С учетом сказанного, матрица Tnможет быть представлена в следующем виде
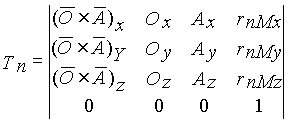
 |
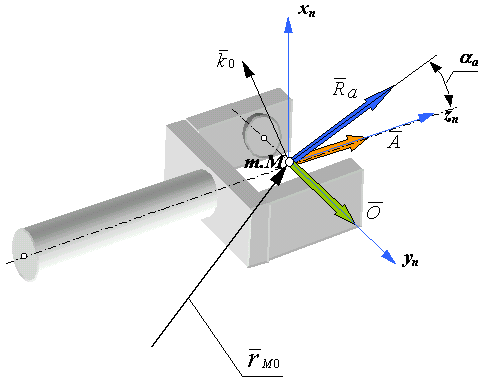 Рис. 20.3 |
В результате матричных преобразований получаем радиус-вектор точки М схвата в функции обобщенных координат. Обычно, за обобщенные координаты принимают линейные и угловые перемещения в кинематических парах или на выходных валах приводов манипулятора. В механизме с n подвижностями в общем виде функцию положения схвата можно записать так
![]()
где q1, q2, ... qn - обобщенные координаты манипулятора.
При кинематическом анализе манипулятора в прямой задаче необходимо определить линейные и угловые скорости и ускорения схвата при заданных угловых и линейных обобщенных скоростях и ускорениях (обычно относительных скоростях и ускорениях в кинематических парах механизма). В обратной задаче по заданному закону изменения скоростей и ускорений схвата определяются законы изменения скоростей и ускорений в КП или на выходных звеньях приводов. Решение прямой задачи кинематики для точки М схвата можно получить продифференцировав четвертый столбец матрицы Тn по времени
 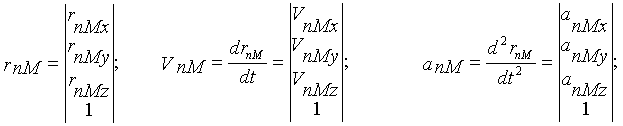 |
Угловую скорость и угловое ускорение схвата можно определить векторным суммированием относительных угловых скоростей во вращательных КП механизма. Так как вектора угловых скоростей, при данном выборе ориентации осей координат, совпадают с осью z, то угловая скорость схвата
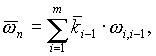
где ![]() орт оси z системы координат, расположенной в центре КП, соединяющей звено i и звено i-1, m - число вращательных КП в механизме.
орт оси z системы координат, расположенной в центре КП, соединяющей звено i и звено i-1, m - число вращательных КП в механизме.
Дифференцируя это выражение по времени, получим формулу для определения углового ускорения схвата:
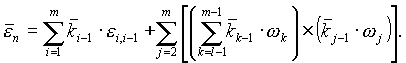
Динамика манипуляторов промышленных роботов.
Силовой расчет манипулятора.
Из большого разнообразия задач динамики манипуляторов рассмотрим две: силовой расчет и расчет быстродействия ПР. При силовом расчете манипуляторов решается задачи по определению внешних силовых управляющих воздействий, обеспечивающих требуемый закон движения механизма, и по расчету реакций в кинематических парах. Первую часть часто называют задачей синтеза управления . При силовом расчете обычно применяется метод кинетостатики, основанный на принципе Д'Аламбера. По этому методу к внешним силам и моментам, приложенным к звеньям механизма, добавляются расчетные силы инерции, которые обеспечивают силовую уравновешенность системы и позволяют рассматривать подвижную систему в квазистатическом равновесии, то есть, как условно неподвижную. Силовой расчет выполняется при заданной полезной нагрузке ![]() , известных законах движения звеньев
, известных законах движения звеньев ![]() и
и ![]() (из предварительного кинематического расчета), известных инерционных характеристиках звеньев: массах звеньев mi и их моментах инерции Isi. По этим данным определяются главные вектора
(из предварительного кинематического расчета), известных инерционных характеристиках звеньев: массах звеньев mi и их моментах инерции Isi. По этим данным определяются главные вектора ![]() и главные моменты
и главные моменты ![]() сил инерции для каждого из звеньев механизма. Для открытой кинематической цепи решение начинаем с выходного звена - схвата. Отброшенные связи звена n со звеном n-1 и выходным валом привода звена n заменяем реакциями
сил инерции для каждого из звеньев механизма. Для открытой кинематической цепи решение начинаем с выходного звена - схвата. Отброшенные связи звена n со звеном n-1 и выходным валом привода звена n заменяем реакциями ![]() и
и ![]() и составляем кинетостатические векторные уравнения равновесия сил и моментов для звена n (Рис.20.4):
и составляем кинетостатические векторные уравнения равновесия сил и моментов для звена n (Рис.20.4):
![]()
![]()
где ![]() - вектор момента в кинематической паре (проекция этого вектора на ось z является движущим моментом привода в КП, то есть
- вектор момента в кинематической паре (проекция этого вектора на ось z является движущим моментом привода в КП, то есть ![]() ).
).
 |
 Рис. 20.4 |
Проецируя векторные уравнения на оси координат, получим систему шести алгебраических уравнений откуда определим шесть неизвестных
![]()
Далее рассматривается равновесие звена n-1. При этом в месте его присоединения к звену n прикладываются реакции со стороны звена n
![]() ,
,
равные по величине и противоположные по направлению реакциям, определенным на предыдущем этапе расчета. Так последовательно составляются уравнения силового равновесия для всех nзвеньев механизма. Из решения полученной системы 6n уравнений определяются реакции в кинематических парах, движущие силы и моменты.
Расчет быстродействия промышленного робота.
Время выполнения роботом цикла перемещений детали во многом определяет производительность всего роботизированного комплекса. Поэтому требования к быстродействию робота обычно достаточно высокие. Время выполнения роботом технологической операции обусловлено законами изменения внешних сил (движущих и сопротивления) и инертностью звеньев механизма. Закон изменения управляющих сил зависит от типа используемого привода и от вида системы управления. Существуют роботы с гидравлическими, пневматическими, электрическими и комбинированными приводами. В них применяются цикловые, позиционные или контурные системы управления. Рассмотрим расчет быстродействия одного из приводов промышленного робота с цикловой системой управления. При цикловой системе управления относительные перемещения звеньев ограничиваются передвижными упорами и концевыми выключателями.
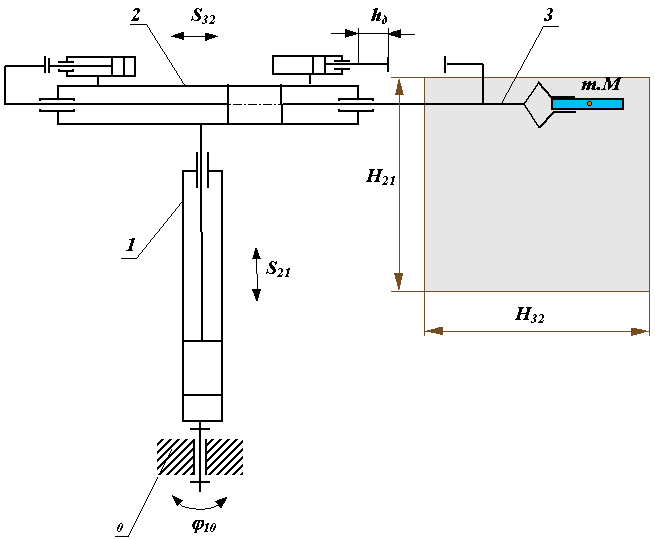
На рис. 20.5 изображена кинематическая схема трехподвижного манипулятора ПР (1,2,3 - подвижные звенья, 0 - неподвижное звено). Здесь же приведена циклограмма настройки командоаппарата (сплошные линии) и циклограмма работы ПР (пунктирные линии). Общее время рабочего цикла Тц состоит из времени выстоя в заданных положениях (на циклограмме выстой показан прямыми параллельными горизонтальной оси t) и времени относительных перемещений звеньев из одного заданного положения в другое tпх и обратно tох (наклоные прямые на диаграммах ). Время выстоя обычно задано условиями технологического процесса. Время выполнения роботом движений определяется динамическими характеристиками приводов и манипулятора - движущими силами и силами сопротивления, массами и моментами инерции звеньев.
  |
Циклограммы командоаппарата и промышленного робота.
 |
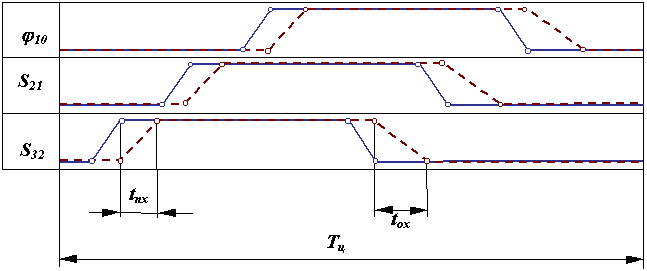 Рис. 20.5 |
Рассмотрим работу пневмопривода перемещения руки манипулятора (рис.20.5). По сигналу от командоаппарата в правую полость цилиндра подается сжатый воздух, который действует на поршень с силой Fд3 = p Ч Sп, где р - давление воздуха, Sп - активная площадь поршня. Под действием этой силы поршень и рука 3 перемещаются влево с постоянным ускорением и с возрастающей скоростью V32 (рис.20.6а). Ограничение хода поршня может осуществляться либо жестким упором без демпфера, либо упором с демпфером.
 |
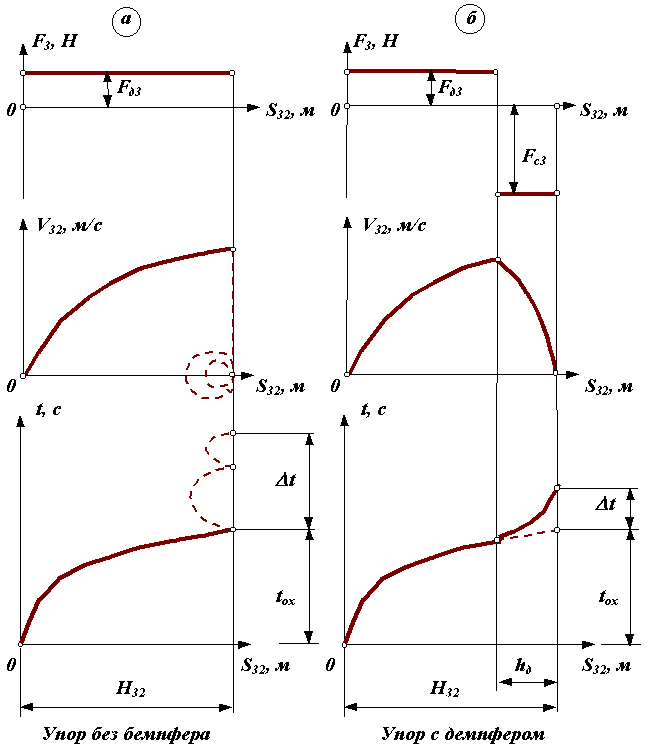 Рис. 20.6 |
При остановке на упоре без демпфера , скорость звена 3 должна мгновенно уменьшится с некоторого конечного значения до нуля. При таком изменении скорости ускорение a32 стремится к бесконечности. Такая остановка звена называется жестким ударом. Она сопровождается большими динамическими нагрузками на звенья механизма. Так как реальный манипулятор представляет собой упруго-инерционную систему, то эти нагрузки вызовут отскок звена 3 от упора, а также колебания всего механизма. Схват будет совершать колебания относительно заданного конечного положения. Время затухания этого процесса Dt (рис.20.6а) значительно снижает быстродействие ПР.
Уменьшить эти колебания или вообще исключить их можно, обеспечив безударный останов
V32n = 0, a32n = 0;
где V32n, a32n - относительная скорость и относительное ускорение звеньев в момент останова. Однако это осуществимо только в регулируемом приводе при контурном управлении. Кроме того при безударном останове в конце хода относительная скорость близка к нулю, поэтому время перемещения схвата в требуемое положение значительно возрастает. Компромиссным решением является останов с мягким ударом, при котором относительная скорость в конце хода V32n= 0, а ускорение ограничено некоторым допустимым значением a32n <= [a] . В механизмах с цикловым управлением режим движения с мягким ударом обеспечивается установкой упоров с демпферами, гасящими кинетическую энергию руки. Расчет демпфера ведется из условия ASn =0 , которое обеспечивается равенством за цикл движения работы движущей силы AFд3 и работы силы сопротивления демпфера АFc (рис. 20.6б):
AFд3 = -АFc или Fд3 * (H32 - hд) = - Fc * hд.
В этом выражении неизвестны две величины Fc и hд, одной из них задаются, вторую - рассчитывают.
Уравновешивание манипуляторов.
В большинстве кинематических схем манипуляторов приводы восприниамают статические нагрузки от сил веса звеньев. Это требует значительного увеличения мощностей двигателей приводов и моментов тормозных устройств. Для борьбы с этим используют три метода:
 |
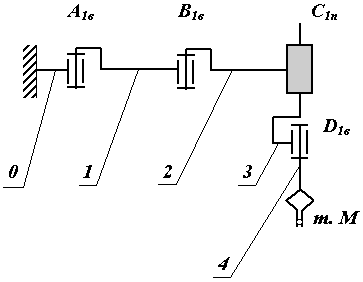 Рис. 20.7 |
 |
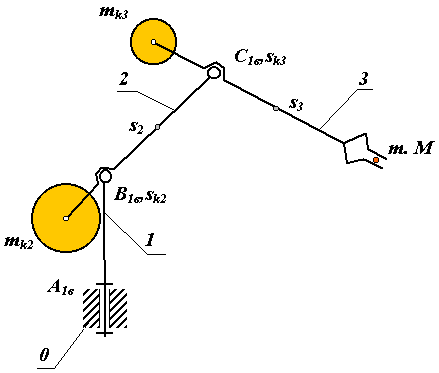 Рис. 20.8 |
 |
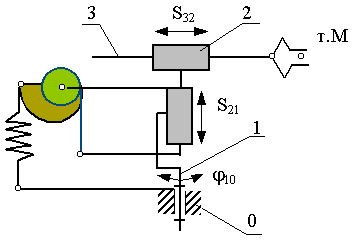 Рис. 20.9 |
Точность манипуляторов ПР.
Точность манипуляторов определяется погрешностями позиционирования характеристической точки схвата (точка М) и погрешностями угловой ориентации схвата. Погрешности позиционирования определяются технологическими отклонениями размеров звеньев манипулятора, зазорами в кинематических парах манипулятора и механизмов приводов, деформациями (упругими и температурными) звеньев, а также погрешностями системы управления и датчиков обратной связи. В паспортных данных манипуляторов указывается максимально допустимое отклонение центра схвата манипулятора точки М от ее номинального расположения на множестве возможных конфигураций механизма. В результате погрешностей точка М описывает в пространстве некоторый эллипсоид, который называется эллипсоидом отклонений (рис. 20.10).
 |
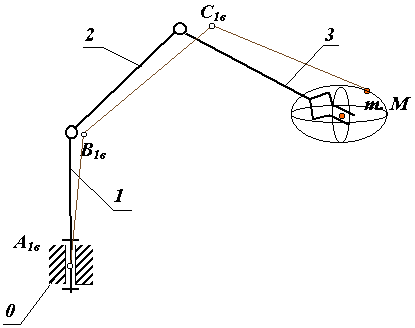 Рис. 20.10 |
1. Каков план применения метода матриц при анализе кинематической цепи манипулятора?(стр.2-5)
2. В какой последовательности проводится силовой расчет манипуляторов? (стр.7-8)
3. Для чего проводится уравновешивание механизмов манипуляторов?(стр.11-13