В результате изучения студент должен знать:
- формулы для расчета сил в зацеплении;
- формулы для расчета прямозубых передач на контактную прочность и изгиб.
4.4.1 Общие сведения
Цилиндрическая прямозубая зубчатая передача относится к передачам зацеплением непосредственного контакта рис.2.3.11. Применяется при окружных скоростях 
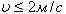 .
.
 ;
;
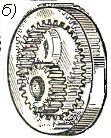
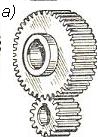
Рисунок 2.3.11 Наружное а) и внутреннее б) зацепление
4.4.2 Силы в зацеплении
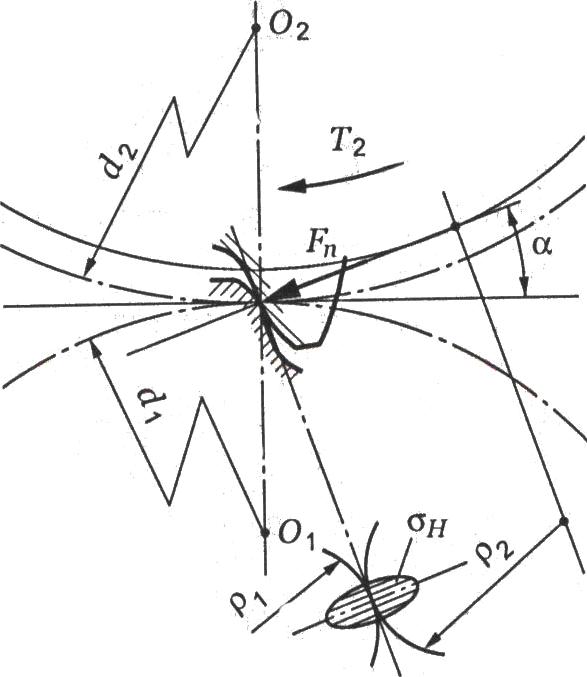
Силы в зацеплении определяют в полюсе зацепления. На шестерню действует вращательный момент, который создаёт распределённую по контактным линиям зуба колеса нагрузку. Эту нагрузку заменяют равнодействующей силой 
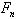 , направленной по линии зацепления nn и приложенной в полюсе. Силами трения в зацеплении пренебрегают, так как они малы. Силу
, направленной по линии зацепления nn и приложенной в полюсе. Силами трения в зацеплении пренебрегают, так как они малы. Силу .JPG)
 раскладывают на окружную Ft и радиальную Fr (рис. 2.3.12):
раскладывают на окружную Ft и радиальную Fr (рис. 2.3.12):

 ;
;
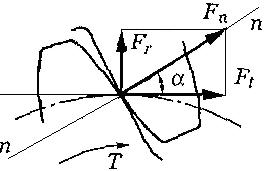
Рисунок 2.3.12 Схема действия сил в зубчатом зацеплении
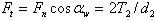

(2.3.14)
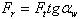

(2.3.15)
Такое разложение силы .JPG) на составляющие удобно для расчёта зубьев и валов. На ведомом колесе направление силы Ft совпадает с направлением вращения, а на ведущем – противоположно ему, т.е. силы на ведущем и ведомом колёсах всегда направлены против действия соответствующих моментов. Радиальные силы Fr направлены к осям вращения колёс и создают "распор" в передаче. Расчет на прочность зубчатых колес проводят по двум условиям прочности: по контактным напряжениям и по напряжениям изгиба. При расчете по контактным напряжениям для всех коэффициентов применяется индекс "Н", по напряжениям изгиба – индекс "F".
на составляющие удобно для расчёта зубьев и валов. На ведомом колесе направление силы Ft совпадает с направлением вращения, а на ведущем – противоположно ему, т.е. силы на ведущем и ведомом колёсах всегда направлены против действия соответствующих моментов. Радиальные силы Fr направлены к осям вращения колёс и создают "распор" в передаче. Расчет на прочность зубчатых колес проводят по двум условиям прочности: по контактным напряжениям и по напряжениям изгиба. При расчете по контактным напряжениям для всех коэффициентов применяется индекс "Н", по напряжениям изгиба – индекс "F".
4.4.3 Расчёт на контактную прочность рабочих поверхностей зубьев
Расчёт на контактную прочность рабочих поверхностей зубьев является основным критерием работоспособности зубчатых передач.
Расчёт производят при контакте зубьев в полюсе зацепления П. Контакт зубьев рассматривают как контакт двух цилиндров с радиусом р1 и р2. При этом наибольшие контактные напряжения определяют по формуле Герца:
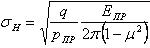

(2.3.16)
Расчет по контактной прочности сводится к проверке условия  . После преобразования формулы Герца для контакта цилиндрических поверхностей получают формулу для определения межосевого расстояния
. После преобразования формулы Герца для контакта цилиндрических поверхностей получают формулу для определения межосевого расстояния
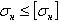

(2.3.17)
где Т2 – вращающий момент на тихоходном валу, Н м;
u - передаточное число;
Ка = 49,5 МПа – для прямозубых колес;

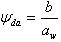 - коэффициент ширины колеса по межцентровому расстоянию, его можно определить по формуле
- коэффициент ширины колеса по межцентровому расстоянию, его можно определить по формуле 
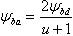 где
где 
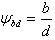 - выбирается из справочных таблиц,
- выбирается из справочных таблиц,  -
- 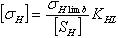 допускаемое контактное напряжение,
где
допускаемое контактное напряжение,
где 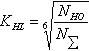 - коэффициент долговечности,
- коэффициент долговечности,
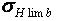 - предел контактной выносливости, определяется для заданного материала из таблиц,
- предел контактной выносливости, определяется для заданного материала из таблиц,

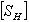 = 1,1- 1,3 - допускаемый коэффициент запаса прочности,
= 1,1- 1,3 - допускаемый коэффициент запаса прочности,

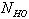 - базовое число циклов нагружения,
- базовое число циклов нагружения,

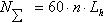 - расчетное число циклов нагружения,
Lh – полный ресурс в час.
Определив геометрические размеры передачи, ее проверяют на контактную прочность по формуле:
- расчетное число циклов нагружения,
Lh – полный ресурс в час.
Определив геометрические размеры передачи, ее проверяют на контактную прочность по формуле: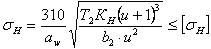

(2.3.18)
где 
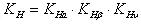 - коэффициент нагрузки при расчете по контактным напряжениям,
- коэффициент нагрузки при расчете по контактным напряжениям,
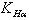
 - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач
- коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач  =1),
=1),

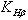 - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий),
- коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий),
.JPG)
 =1,25 - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки.
=1,25 - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки.
4.4.4 Расчёт зубьев на изгиб
Поломка зубьев связана с напряжениями изгиба, вследствие усталости материала от длительно действующих нагрузок. Расчет на изгиб сводится к проверке условия:
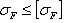

(2.3.19)
При выводе расчётной формулы для определения напряжений изгиба принимают следующие допущения:
1) вся нагрузка 
.JPG) зацепления передаются одной парой зубьев, которая приложена к вершине зуба и направлена по нормали к его профилю (сила трения не учитываются); 2) зуб рассматривают как консольную балку прямоугольного сечения, что позволяет рассчитывать его методами сопротивления материалов. Фактически зуб представляет собой балку с изменяющейся формой. Это учитывается введением в расчётные формулы теоретического коэффициента концентрации напряжений Кт.
зацепления передаются одной парой зубьев, которая приложена к вершине зуба и направлена по нормали к его профилю (сила трения не учитываются); 2) зуб рассматривают как консольную балку прямоугольного сечения, что позволяет рассчитывать его методами сопротивления материалов. Фактически зуб представляет собой балку с изменяющейся формой. Это учитывается введением в расчётные формулы теоретического коэффициента концентрации напряжений Кт.
Распределённую по ширине венца зуба нагрузку заменяют сосредоточенной силой .JPG)
 , которую переносят по линии действия на ось зуба и раскладывают на две составляющие: изгибающую зуб
, которую переносят по линии действия на ось зуба и раскладывают на две составляющие: изгибающую зуб 
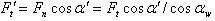 и сжимающую
и сжимающую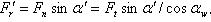
 , где
, где 
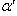 - угол направления нормальной силы Fn. Он несколько больше угла зацепления
- угол направления нормальной силы Fn. Он несколько больше угла зацепления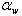
 .
.
Напряжение изгиба в опасном сечении (вблизи хорды основной окружности), т.е. напряжение на растянутой стороне зуба, где возникают усталостные трещины рис.2.3.13.
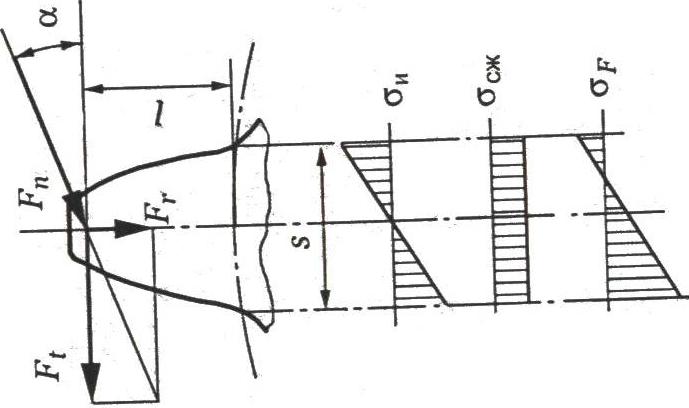
Рисунок 2.3.13 Эпюры распределения напряжений по ширине зуба
Напряжения определяются отношением внешней силы к моменту сопротивления сечения.
Тогда после подстановки в исходную формулу, формула проверочного расчёта прямозубых передач:
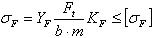
 (2.3.20)
(2.3.20)
где 
.JPG) и
и 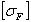
 - расчётное и допускаемое напряжения изгиба, Н/мм2.
Ft – окружная сила, H,
b и m – ширина и модуль зубчатого колеса или шестерни, мм,
YF – коэффициент формы зуба – величина безразмерная, зависящая от числа зубьев z или zv и коэффициента смещения х. Значения YF для зубчатых колёс без смещения приводятся в справочнике,
- расчётное и допускаемое напряжения изгиба, Н/мм2.
Ft – окружная сила, H,
b и m – ширина и модуль зубчатого колеса или шестерни, мм,
YF – коэффициент формы зуба – величина безразмерная, зависящая от числа зубьев z или zv и коэффициента смещения х. Значения YF для зубчатых колёс без смещения приводятся в справочнике,
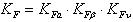
 -коэффициент нагрузки при расчете на изгиб,
-коэффициент нагрузки при расчете на изгиб,
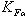
 - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач
- коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач  ),
),

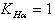 - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий),
- коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий),

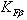 - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки,
- коэффициент нагрузки, учитывающий дополнительные динамические нагрузки,

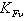 - допускаемое напряжение изгиба,
- допускаемое напряжение изгиба,

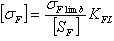 - предел выносливости зубьев при изгибе,
- предел выносливости зубьев при изгибе,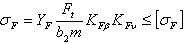

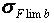 - коэффициент долговечности при изгибе,
- коэффициент долговечности при изгибе,
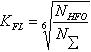
 - базовое число циклов при изгибе,
- базовое число циклов при изгибе,

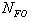 = 1,55- 1,75 - допускаемый коэффициент запаса прочности,
= 1,55- 1,75 - допускаемый коэффициент запаса прочности,
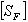 Зубья шестерни и колеса будут иметь примерно равную прочность на изгиб при условии
Зубья шестерни и колеса будут иметь примерно равную прочность на изгиб при условии
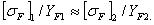

(2.3.21)
Модуль зубьев m определяют расчётом на изгиб, исходя из межосевого расстояния 
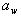 , полученного из условия контактной прочности. В этом случае для получения расчётной формулы надо в выражении (2.3.20):
, полученного из условия контактной прочности. В этом случае для получения расчётной формулы надо в выражении (2.3.20): 
.JPG) заменить ft на 2Т/d, где
заменить ft на 2Т/d, где 
.JPG) . Тогда, решив уравнение
. Тогда, решив уравнение .JPG)
 относительно модуля m, при некоторых средних значениях коэффициентов
относительно модуля m, при некоторых средних значениях коэффициентов 
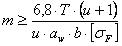 ,
, 
.JPG) и
и 
.JPG) получим формулу для приближенного определения модуля:
получим формулу для приближенного определения модуля:
.JPG)
 (2.3.22)
(2.3.22)
В эту формулу вместо 
.JPG) подставляют меньшее из
подставляют меньшее из 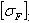
 и
и 
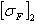 . Полученное значение модуля округляют в большую сторону до стандартного. Модуль колес рекомендуется принимать минимальным. Уменьшение модуля и соответствующее увеличение числа зубьев способствует уменьшению удельного скольжения, что увеличивает надежность против заедания. При малом модуле увеличивается коэффициент торцевого перекрытия
. Полученное значение модуля округляют в большую сторону до стандартного. Модуль колес рекомендуется принимать минимальным. Уменьшение модуля и соответствующее увеличение числа зубьев способствует уменьшению удельного скольжения, что увеличивает надежность против заедания. При малом модуле увеличивается коэффициент торцевого перекрытия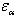
 . То есть увеличивается плавность работы зацепления и к.п.д., уменьшается шум.
. То есть увеличивается плавность работы зацепления и к.п.д., уменьшается шум.
.

 ;
;

, направленной по линии зацепления nn и приложенной в полюсе. Силами трения в зацеплении пренебрегают, так как они малы. Силу


 ;
;



 . После преобразования формулы Герца для контакта цилиндрических поверхностей получают формулу для определения межосевого расстояния
. После преобразования формулы Герца для контакта цилиндрических поверхностей получают формулу для определения межосевого расстояния



 -
- 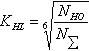 - коэффициент долговечности,
- коэффициент долговечности,




 - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач
- коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач  =1),
=1), 
 =1,25 - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки.
=1,25 - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки.
зацепления передаются одной парой зубьев, которая приложена к вершине зуба и направлена по нормали к его профилю (сила трения не учитываются); 2) зуб рассматривают как консольную балку прямоугольного сечения, что позволяет рассчитывать его методами сопротивления материалов. Фактически зуб представляет собой балку с изменяющейся формой. Это учитывается введением в расчётные формулы теоретического коэффициента концентрации напряжений Кт.

и сжимающую

- угол направления нормальной силы Fn. Он несколько больше угла зацепления


 (2.3.20)
(2.3.20)
 - расчётное и допускаемое напряжения изгиба, Н/мм2.
- расчётное и допускаемое напряжения изгиба, Н/мм2.  -коэффициент нагрузки при расчете на изгиб,
-коэффициент нагрузки при расчете на изгиб, - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач
- коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач  ),
), 




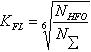
 - базовое число циклов при изгибе,
- базовое число циклов при изгибе,




 относительно модуля m, при некоторых средних значениях коэффициентов
относительно модуля m, при некоторых средних значениях коэффициентов 


 (2.3.22)
(2.3.22)
 и
и 
 . То есть увеличивается плавность работы зацепления и к.п.д., уменьшается шум.
. То есть увеличивается плавность работы зацепления и к.п.д., уменьшается шум.