Коническая зубчатая передача

В результате изучения студент должен знать:

- геометрические параметры конической передачи;
- формулы для расчета сил в зацеплении;
- формулы для расчета конических передач на контактную прочность и изгиб.

4.6.1 Общие сведения

Конические зубчатые колёса применяют в передачах, оси валов которых пересекаются под некоторым межосевым углом . Обычно рис.2.3.17.

Рисунок 2.3.17 Коническая прямозубая передача а), передача с круговым зубом б)

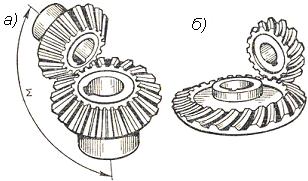
Применяют во всех отраслях машиностроения, где по условиям компоновки машины необходимо передать движение между пересекающимися осями валов. Конические передачи сложнее цилиндрических, требуют периодической регулировки. Для нарезания зубчатых конических колес необходим специальный инструмент. В сравнении с цилиндрическими конические передачи имеют большую массу и габарит, сложнее в монтаже. Кроме того, одно из конических колёс, как правило шестерня, располагается консольно. При этом, вследствие повышенной деформации консольного вала, увеличиваются неравномерность распределения нагрузки по ширине зубчатого венца и шум.

Конические колёса бывают с прямыми и круговыми зубьями.

Передаточное числа при межосевом угле

(2.3.44)

Для конической прямозубой передачи рекомендуется u = 2, 2,5; 3,15; 4, для передачи с круговыми зубьями возможны более высокие значения u; наибольшее значение u = 6,3.

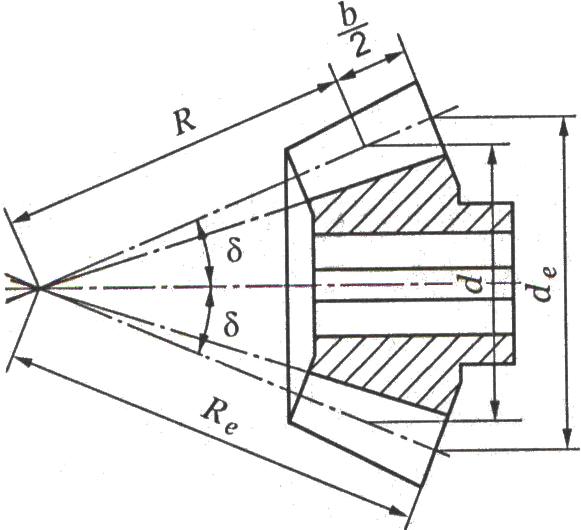
4.6.2 Геометрические параметры конического зубчатого колеса

Основные геометрические размеры определяют в зависимости от модуля и числа зубьев. Высота и толщина зубьев конических колёс постепенно уменьшается по мере приближения к вершине конуса. Соответственно изменяются шаг, модуль и делительные диаметры, которых может быть бесчисленное множество. Основные геометрические размеры имеют обозначения, принятые для прямозубых конических передач рис. 2.3.18.

Рисунок 2.3.18 Геометрия конического колеса

Внешний диаметр

(2.3.45)

где

- максимальный модуль зубьев – внешний окружной модуль, полученный по внешнему торцу колеса. Внешнее конусное расстояние

(2.3.46)

Среднее конусное расстояние

(2.3.47), где b – ширина зубчатого венца колеса

(2.3.48)

- коэффициент ширины зубчатого венца относительно внешнего конусного расстояния.

- углы делительных конусов;
Средний модуль

(2.3.49)

Средние делительные диаметры:

(2.3.50)

(2.3.51)

В соответствии с исходным контуром прямозубых конических колёс радиальный зазор c = 0,2

, тогда
внешняя высота головки зуба

(2.3.52)
и внешняя высота ножки зуба

(2.3.53).

Внешние диаметры вершин зубьев

(2.3.54)

(2.3.55)

Угол ножки зуба

(2.3.56).

Угол головки зуба

;

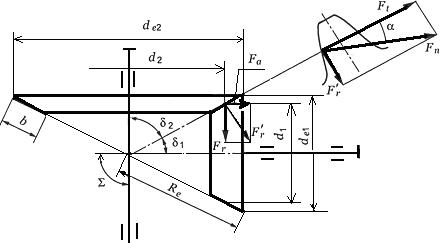
(2.3.57)

4.6.3 Силы в зацеплении конической передачи

Силы в зацеплении определяют по размерам в среднем сечении зуба шестерни. На шестерню конической прямозубой передачи действуют три силы рис.2.3.19:
окружная  (2.3.58),
радиальная  (2.3.59),
осевая  (2.3.60).

Рисунок 2.3.19 Схема действия сил в зацеплении конических колес

Для колеса направление сил противоположно, при этом:

;

Направление окружных сил F, как и в цилиндрической передаче зависит от направления вращения колёс. Осевые силы всегда направлены от вершин конусов, радиальные - к осям вращения колёс. Конические передачи с круговыми зубьями получили преимущественное применение. По сравнению с коническими прямозубыми они менее чувствительны к нарушению точности взаимного расположения колёс, их изготовление проще. Недостаток передач с круговыми зубьями – изменение величины и знака осевых сил при реверсе. Ось кругового зуба – это дуга окружности соответствующего диаметра резцовой головки. Нарезание зубьев резцовой головки обеспечивает высокую производительность и низкую стоимость колёс. Угол наклона кругового зуба переменный. За расчётный принимают угол на окружности среднего диаметра колеса, обычно Значение выбирают исходя из обеспечения плавности зацепления.

4.6.4 Расчет на контактную прочность

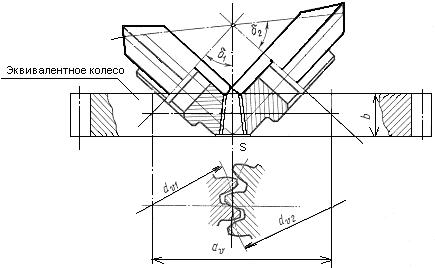
Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же как у эквивалентного цилиндрического. Эквивалентным колесом называется такое цилиндрическое колесо, у которого делительный диаметр и модуль равны делительному диаметру и модулю в среднем нормальном сечении реального конического колеса рис.2.3.20.