Проектирование кулачковых механизмов графическим методом

Проектирование ведется в последовательности, которая указана в разделе 1.

1. Построение кинематических диаграмм методом графического интегрирования.

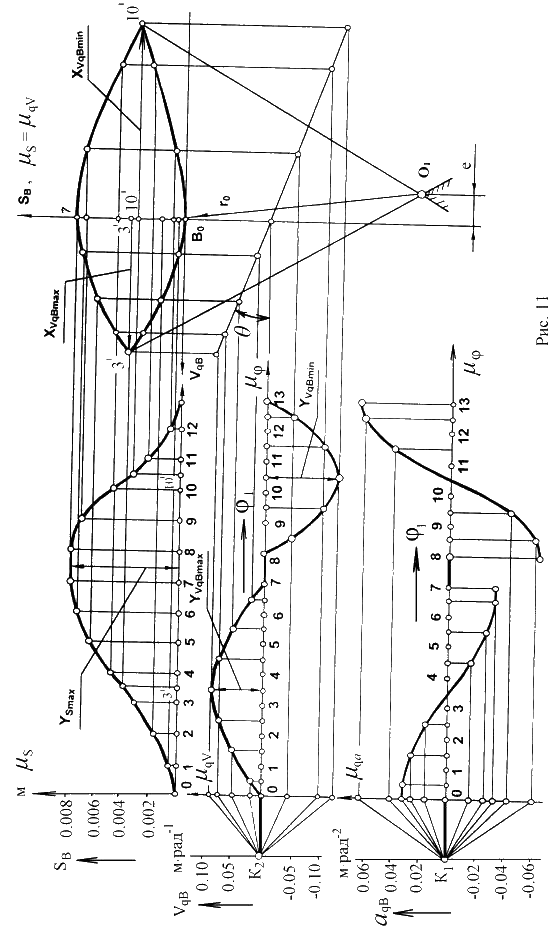
Построение начинают с заданного графика кинематической передаточной функции ускорения (рис. 3а, 11а). По оси абсцисс откладывают фазовые углы j_1У + j_1Д + j_1С = j_Р

Масштаб по оси j вычисляют по формуле м/рад ,

где j_1p - угол рабочего профиля, град.,

b - база графиков, мм.

Максимальное значение ординаты графика на фазе удаления задают произвольно, а максимальное значение ординаты на фазе сближения вычисляют по условию равенства площадей из пропорции .

Методом графического интегрирования строят график кинематической передаточной функции скорости толкателя. Для этого на продолжении оси j₁ графика a_qB(j₁) выбирают произвольный отрезок интегрирования K₁, делят ось абсцисс графика на интервалы, из середины каждого интервала восстанавливают перпендикуляр к оси j₁ до пересечения с кривой a_qB(j₁) ,

Таблица 6.

РЕЗУЛЬТАТЫ РАСЧЕТА КУЛАЧКОВОГО МЕХАНИЗМА С КАЧАЮЩИМСЯ ТОЛКАТЕЛЕМ

ВАРИАНТ А

ИСХОДНЫЕ ДАННЫЕ: Н=.020 FIR=130.0 WR=0 UTD=30.0 L2=.030

РЕЗУЛЬТАТЫ РАСЧЕТА: RO=.0533 A=.0716

FIK=30.0 VQK=.026 SK=.008

FIN=100 VQN=-.036 SN=.013

I	FI1	AQ	VQ	S
0	.0	15.000	.000	.000
1	10.0	13.000	.011	.000
2	20.0	10.000	.020	.004
3	30.0	3.000	.026	.008
4	40.0	-3.000	.026	.012
5	50.0	-10.000	.020	.016
6	60.0	-13.000	.011	.019
7	70.0	-15.000	.000	.020
8	80.0	.000	.000	.020
9	90.0	-25.000	-.022	.018
10	100.0	-10.000	-.036	.013
11	110.0	10.000	-.036	.007
12	120.0	25.000	-.022	.002
13	130.0	30.000	.000	.000

I	PSI	R	XB	YB	TET
0	0.	.0533	.0533	.0000	25.6664
1	10.4	.0542	.0533	-.0098	33.3188
2	21.4	.0568	.0529	-.0207	34.3708
3	32.3	.0607	.0513	-.0324	30.0000
4	42.6	.0652	.0480	-.0441	21.2215
5	52.3	.0692	.0423	-.0548	9.2179
6	61.9	.0719	.0338	-.0635	-3.6515
7	71.8	.0729	.0228	-.0692	-14.2965
8	81.8	.0729	.0104	-.0721	-14.2963
9	92.1	.0710	-.0026	-.0710	-27.0112
10	102.6	.0660	-.0144	-.0644	-30.0000
11	112.1	.0597	-.0225	-.0553	-23.0417
12	120.7	.0548	-.0280	-.0472	-1.8520
13	129.7	.0531	-.0340	-.0407	26.3327

средние значения ординат на каждом шаге проецируют на ось ординат и полученные точки соединяют с концом выбранного отрезка интегрирования.

Лучи, выходящие из точки конца отрезка интегрирования K₁, характеризуются углами наклона, которые равны углам наклона касательных, проведенных в соответствующих точках к искомой интегральной кривой V_qB(j₁). Кривую V_qB(j₁) строят, проводя на каждом интервале отрезок, параллельный соответствующему лучу исходного графика a_qB(j₁) .Аналогично строят зависимость перемещения толкателя от угла поворота кулачка S_B(j₁) графическим интегрированием диаграммы V_qB(j₁), выбрав отрезок интегрирования K₂.

Вычисляют масштабы по осям ординат построенных графиков S_B , V_qB и a_qB , используя известные соотношения (2,5...7) при графическом интегрировании.

2. Определение основных размеров кулачкового механизма.

Основные размеры механизма определяют с помощью фазового портрета, представляющего собой зависимость S_B(V_qB). Масштабы, выбранные по оси S_B (перемещений) и оси V_qB должны быть одинаковыми. Для механизма с поступательно перемещающимся толкателем фазовый портрет строят в декартовой системе координат (рис. 11, б). с вращающимся толкателем - в полярной системе (рис. 12). По оси S_B откладывают перемещения толкателя - в первом случае от начала координат в точке B₀ вдоль линии перемещения толкателя , во втором - от точке В₀ по дуге радиуса L₂. проходящей через эту точку. Отрезки, соответствующие перемещениям толкателя откладывают, либо в масштабе m_S графика перемещений, либо в масштабе

кинематической передаточной функции скорости.

Рис. 11

От полученных точек откладывают отрезки кинематических передаточных функций выбранном масштабе, соответственно перпендикулярно линии перемещения толкателя и вдоль толкателя.

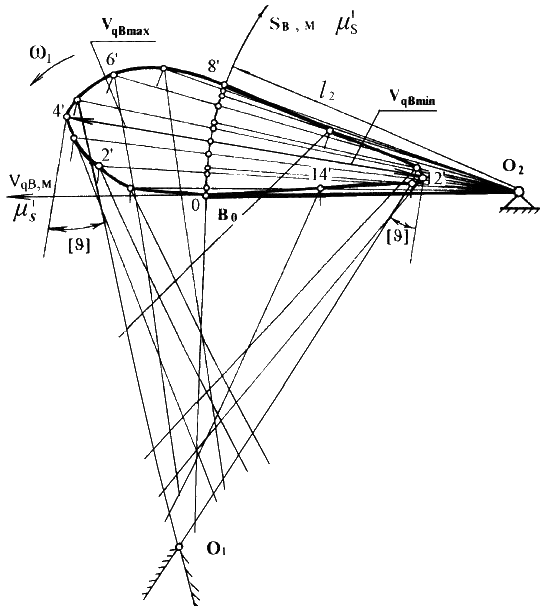
Длины отрезков, изображающих кинематические передаточные функции скорости толкателя , вычисляют по формуле

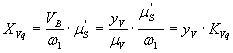мм,

Для определения направления вектора передаточной функции скорости следует вектор скорости толкателя повернуть на 90° в сторону вращения кулачка. При этом значение передаточной функции считается положительным при удалении толкателя и отрицательным при сближении.

Для удобства построения фазового портрета значения следует свести в таблицу 7.

Таблица 7

Номер позиции
Величина	1	2	3	...
Y_V, мм
m^'_s / m_V×w₁=K_Vq величина постоянная
X_Vq = K_VqY_V, мм

Фазовый портрет для механизма с поступательно движущимся толкателем можно построить и методом графического исключения параметра j₁ из диаграмм S_B(j₁), V_qB(j₁). Для этого проводят вертикальную прямую - ось S_B графика S_B(V_qB) (рис. 11б), продолжают ось j₁ графика V_qB(j₁) до пересечения с осью S_B, через полученную точку пересечения проводят прямую под углом q =arctg(m_qv / m_s) к горизонтали таким образом, чтобы при дальнейшем построении направление вектора передаточной функции соответствовало направлению вращения кулачка. Фазовый портрет строят по точкам. Для выбранной позиции проводят через точку графика V_qB(j₁) горизонталь до пересечения с прямой, проведенной под углом q, и через полученную точку - вертикаль. Через точку графика S_B(j₁) в той же позиции проводят горизонтальную прямую до пересечения с построенной вертикалью. Точка пересечения - точка графика S_B(V_qB) в выбранной позиции. Аналогично получают все остальные точки графика, которые соединяют плавной кривой.

Рис. 12

Если реверсивное движение кулачка не предусмотрено и значения углов давления на фазе сближения не заданы, достаточно построить только одну ветвь фазового портрета, соответствующую удалению толкателя.

Фазовый портрет для механизма с поступательно перемещающимся толкателем ограничивают в характерных точках лучами, которые проводят под заданными допустимыми углами давления к перпендикулярам, восстановленным в этих точках к векторам кинематических передаточных отношений.

На фазовом портрете механизма с качающимся толкателем лучи проводят в каждом положении. Внутри ограниченной лучами области допустимых решений выбирают положение оси вращения кулачка O₁ и определяют искомые размеры кулачкового механизма r₀, e или r₀ и a_w.

3. Построение профиля кулачка.

При графическом построении профиля кулачка применяют метод обращения движения: всем звеньям механизма условно сообщают угловую скорость, равную - w₁. При этом кулачок становится неподвижным, а остальные звенья вращаются с угловой скоростью, равной, но противоположной по направлению угловой скорости кулачка.

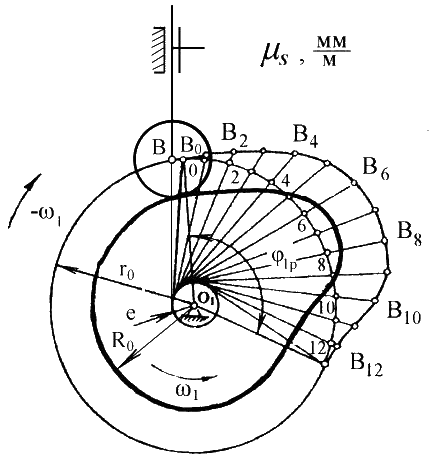
При построении профиля кулачка с внеосным поступательно движущимся толкателем (рис. 13), из центра O₁ проводят окружности радиусами r₀ и e в произвольном масштабе . Касательно к окружности радиуса е проводят линию перемещения толкателя, располагая ее по отношению к центру вращения кулачка таким же образом, как на фазовом портрете и как задано в исходных данных (слева или справа). Точку пересечения линии перемещения толкателя с окружностью радиуса r₀ - B₀ соединяют с центром О₁. От полученного луча O₁B₀ в направлении w₁откладывают угол рабочего профиля кулачка j_1p. Дугу, соответствующую углу j_1p делят на части в соответствии с делением оси j₁ на графике S_B(j₁). Через точки деления 1,2,3,... касательно к окружности радиуса е проводят лучи, являющиеся положениями толкателя в обращенном движении. От точек 1,2,3,... , лежащих на окружности радиуса r₀ , вдоль проведенных лучей откладывают в масштабе m_l перемещения толкателя в каждой позиции. Соединяя полученные точки плавной кривой, получают теоретический (центровой) профиль кулачка.

Рис. 13

При построении профиля кулачка с качающимся толкателем (рис.14) из центра O₁ проводят в масштабе m_l окружности радиусами r₀ и a_w. Точку O₁ соединяют с произвольно выбранной точкой O₂₀ на окружности радиуса a_w. От луча O₁O₂₀ в направлении -w₁ откладывают угол рабочего профиля кулачка j_1p.

Рис. 14

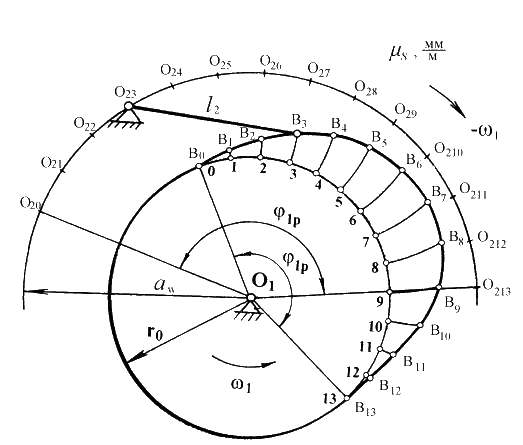
Дугу, соответствующую углу j_1p делят на части в соответствии с делением оси j₁ на графике S_B(j₁). Из точек O₂₀,O₂₁,O₂₂,... проводят дуги радиусом l₂ от точек 0,1,2,... на окружности радиуса r₀. От точек 0, 1, 2, ... по дугам откладывают в масштабе перемещения точки В толкателя - S_B. Соединяя полученные точки В₀ ...В_к плавной кривой, получают теоретический профиль кулачка. Из прочностных или геометрических соображений выбирают радиус ролика, учитывая соотношения

R_P = (0,25-0,4) r₀; или R_P < 0,8 r_min,

где r_min - минимальный радиус кривизны центрового профиля кулачка.

Для получения конструктивного (рабочего) профиля кулачка строят эквидистантный профиль, отстоящий от центрового на величину радиуса ролика. Он получается как огибающая к дугам, проведенным из произвольных точек центрового профиля радиусом ролика (рис 15, 16).

Если технология изготовления кулачка предусматривает использование дуг окружностей, то найденный конструктивный профиль следует заменить профилем, составленным из дуг окружностей. Дуги окружностей должны соответствовать полученному профилю в пределах требуемой точности построений.

При такой замене следует помнить, что кулачок с профилем, составленным из дуг окружностей, всегда дает ступенчатый график ускорений, а график скорости всегда получается с изломом и только график перемещений может быть плавным. Это следует учитывать при выборе числа заменяющих дуг окружностей.

Иногда в кулачковых механизмах по технологическим соображениям рабочая поверхность ведомого звена (толкателя) выполняется плоской. При вращательном движении кулачка использование плоских толкателей возможно лишь в тех случаях, когда радиус кривизны теоретического профиля не меняет своего знака, т.е. не имеет вогнутых участков [5].

Кроме плоских кулачковых механизмов, в практике машиностроения и приборостроения, используются и пространственные кулачковые механизмы. Примером пространственных кулачков могут служить кулачки барабанного типа, широко применяемые в автоматах. На поверхности кулачка, выполненного в виде цилиндра, конуса или гиперболоида вращения, имеется паз для ролика толкателя. В счетно-решающих устройствах употребляются пространственные кулачки-коноиды с двумя независимыми перемещениями [4]. Соответствующая рабочая поверхность такого коноида позволяет механически осуществлять требуемую зависимость угла поворота толкателя как функцию двух аргументов. Алгоритмы расчетов методы проектирования таких кулачковых механизмов приводятся в [2,3,5].