Качественные показатели зубчатых передач

Введением коэффициентов скольжения зубьев l_1,2 учитывается влияние геометрических и кинематических факторов на проскальзывание профилей в процессе зацепления. Наличие скольжения профилей и давления одного профиля на другой при передаче сил приводит к износу профилей. Для объективной оценки скольжения, а следова тельно, и износа эвольвентных профилей зубьев пользуются отношением скорости скольжения и скорости точки контакта по профилю соответственно шестерни и колеса l=n_ск / n^t. В зубчатой передаче необходимо учитывать то, что зубья большего зубчатого колеса зацепляются в U₁₂ раз меньше, чем зубья шестерни, поэтому выражения для коэффи циентов скольжения примут вид:

     для шестерни

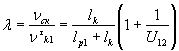(1.34)

     для колеса

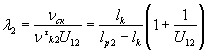(1.35)

     О качестве передачи принято судить по максимальным значениям коэффициентов скольжения в точках начала зацепления (В₁) и конца зацепления (В₂):

в точке В₁

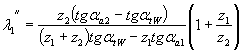>(1.36)

в точке В₂

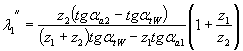(1.37)

Коэффициент удельного давления J учитывает влияние радиусов кривизны профилей зубьев на контактные напря жения. Если эвольвентные поверхности зубьев приближенно принять за поверхности круглых цилиндров, радиусы которых равны радиусам кривизны соответствующих эвольвентных поверхностей в точке их контакта, то для опре деления возникающего при этом контактного напряжения можно использовать известную формулу Герца:

где F_Ht -  равнодействующая распределенной нагрузки по контактной линии, направленная по линии зацепления;  E=2E₁E₂/(E₁+E₂) - приведенный модуль упругости (здесь Е₁, Е₂- модули упругости материалов колес);                       1/r ^пр =1/r₁  +1/r₂ - приведенная кривизна (здесь r₁, r₂ - радиусы кривизны эвольвентных профилей колес в точке контакта, мм); b_W - рабочая ширина зубчатых колес, мм.

     Влияние геометрической формы зуба на удельное давление, независимо от значения модуля, отражается через коэффициент удельного давления J=m/r ^пр, поэтому

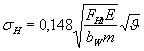
     В подкоренном выражении формулы Герца, записанной в измененном виде, содержатся два сомножителя. Второй сомножитель J зависит от формы зубьев, следовательно, форма зубьев оказывает влияние на контактные напряжения при конкретных нагрузке и материале зубчатых колес. Отметим, что коэффициент удельного давления характеризует не отдельное колесо, а взаимодействие двух зубчатых колес.

     За расчетный коэффициент удельного давления принимают такой, который соответствует контакту зубьев в полюсе зацепления:

(1.39)

     Учет удельного давления наиболее важен для передач, работающих в режиме жидкостного трения.

     Коэффициент перекрытия e позволяет оценивать непрерывность и плавность зацепления в передаче. Эти качества передачи обеспечиваются перекрытием по времени в работе двух пар зубьев: каждая последующая пара зубьев должна войти в зацепление до того, как предшествующая пара выйдет из него. О величине перекрытия в прямозубой передаче судят по коэффициенту торцового перекрытия, выражающему отношение угла торцового перекрытия зубчатого колеса к его угловому шагу (рис. 3, а).

     Нормально работающая прямозубая передача должна иметь коэффициент перекрытия больше единицы. По схеме рабочего зацепления определяют длину активной линии зацепления

g_a = B₁B₂ = (N₂B₁ -PN₂) + (N₁B₂ -PN₁)

                       или

g_a = r_b2 (tga_a2 - tga_tW) + r_b1 (tga_a1 - tga_tW)

где a_a1 и a_a2 - углы профилей на окружностях вершин зубьев колес.

     C учетом того, что p_b =2pr_b1 /z₁ = 2p r_b2 /z₂, получим формулу для коэффициента перекрытия в окончательном виде

(1.40)

 

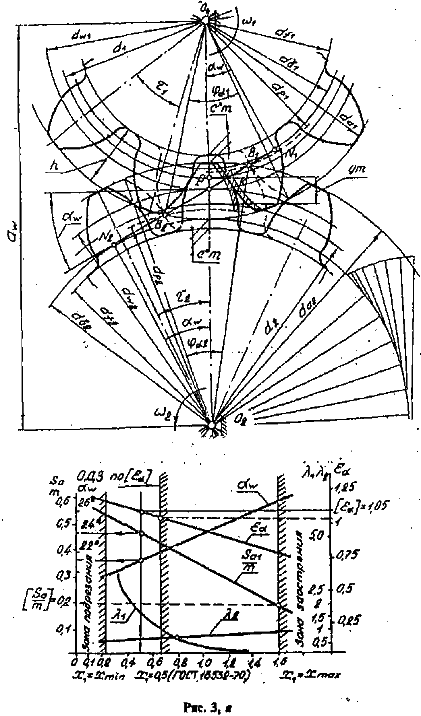
     Коэффициент перекрытия у косозубой передачи при прочих равных условиях больше, чем у прямозубой передачи, вследствие того, что пара зубьев входит в зацепление не одновременно по всей своей длине, а постепенно. Таким образом, увеличивается продолжительность работы одной пары зубьев. Этот немаловажный фактор свидетельствует в пользу применения косозубой передачи, особенно при увеличении степени точности изготовления колес. Формула для определения коэффициента перекрытия косозубой передачи имеет вид

(1.41)

где e_b - коэффициент осевого перекрытия; y_b=b_W /m - коэффициент ширины зубчатого венца, выбираемый из условий прочности и износостойкости зуба.

     Наряду с описанными выше качественными показателями в теории эвольвентной зубчатой передачи анализируются коэффициент ускоренного скольжения, коэффициент формы зуба, а также коэффициент, характеризующий размещение полюса в зоне двухпарного касания. Эти качественные показатели в вузовском курсе "Теория механизмов и машин" не рассматриваются, но они детально описаны в работах [1, 2, 7, 8]. Что же касается коэффициента формы зуба, то достаточно знать, что он всегда уменьшается при увеличении смещения инструмента. Однако нужно помнить, что чрезмерное смещение может привести к заострению зуба [5].