|
Профили зубьев при нарезании методом огибания содержат три характерных участка (рис. 5): 1) а - а, являющийся огибающим по отношению к профилю зубьев инструмента; 2) b - с, очерченный по дуге окружности и представляющий дно впадины; 3) участокb - а, очерченный так называемой переходной кривой. Переходной поверхностью называют часть боковой поверхности зуба, которая соединяет его главную (эвольвентную) поверхность с поверхностью впадин. Часть профиля зуба, расположенную в пределах его переходной поверхности, называют переходной кривой. Форма переходной поверхности, определяет размеры зуба у основания и характеризует, таким образом, изгибную прочность зуба, а также правильного, без интерференции, зацепления с сопряженным колесом и выполнения некоторых видов отделочных, операций. |
Уравнение профиля дает возможность выполнить точное построение профиля в любом требуемом масштабе, не прибегая к графическим способам, описанным в гл. I, § 7. Наличие точных изображений профилей значительно облегчает нахождение коэффициентов концентрации напряжений для зубьев, нарезанных со смещением.
Для построения эвольвентного профиля воспользуемся методикой, изложенной в работе [6]. Пусть имеется прямоугольная система координат (см. рис. 5), ось ординат которой проходит через середину зуба, а начало координат лежит на окружности впадин. В качестве текущего параметра примем не угол развернутости эвольвенты, а угол обкатки инструмента или угол поворота колеса при нарезаний. В предлагаемой системе координат просто выразить толщину зуба и описать переходную кривую профиля зуба колеса, нарезаемого реечным инструментом.
Вывод основных уравнений профиля базируется на методе преобразования координат, отражающем кинематику
|
образования профиля с помощью инструмента, работающего по методу обкатки. Этот метод нарезания основан на том, что по станочно - начальной (делительной) окружности, являющейся в процессе нарезания центроидой, зуборезный инструмент обкатывается без скольжения с помощью своей центроиды. Центроидой у рейки является прямая, у долбяка - окружность. На рис. 6 изображены расчетная схема станочного зацепления, а также неподвижная x0O1y0 и подвижная x¢A у¢системы координат. Ось O1y0 неподвижной системы координат проходит через точку Р пересечения профиля с делительной окружностью, а начало координат 01 находится в центре вращения нарезаемого колеса. |
|
Ось Аx¢ подвижной системы координат совпадает с делительной прямой рейки, а начало координат лежит в точке А на режущей кромке ВС инструмента.
Формулы преобразования для перехода от координат x0O1y0 к координатам x¢A у¢ имеют вид
| x¢ = x0 cosj - y0 sinj + rj ;
y¢ = x0 sinj + y0 cosj - r, |
(1.42) |
или
| x0 = (x¢ - rj) cosj + (y¢ + r) sinj ;
y0 = -( x¢ - rj) sinj + (y¢ + r) cosj. |
(1.43) |
Координаты точки Э, лежащей на нарезаемой эвольвенте профиля в системе координат x¢A у¢:
| xЭ = r×j × sin2j
yЭ = r×j × sinj × cosj |
(1.44) |
Подставляя их в выражение (1.43), получим уравнение эвольвентного профиля в системе х0 01 у0 :
| x0Э = r [ sinj - j cosa cos(j + a ) ]
y0Э = r [ cosj - j cosa sin(j + a ) ] |
(1.45) |
Перейдем теперь к упомянутой ранее системе координат хOу (см. рис. 5), ориентированной относительно середины зуба. Формулы перехода от системы х0 01 у0
| x = x0 cosy - y0 siny
y = y0 siny + y0 cosy - r face="Trebuchet MS">f |
(1.46) |
где y = s /(2r) - половина угловой толщины зуба на делительной окружности; rf - радиус окружности впадин нарезаемого колеса.
С учетом уравнений (1.43) и (1.46) формулы для перехода в систему хОу предстанут в следующем виде:
| x = ( x¢ - rj ) cos( j - y ) + ( y¢ + r ) sin( j - y );
y = -( x¢ - rj ) sin( j - y ) + ( y¢ + r ) cos( j - y ) - rf ; |
(1.47) |
а в системе х' Ау' уравнение эвольвенты будет иметь такую форму:
| xЭ = r [sin( j - y )-j cosa cos(j - y + a )] ;
yЭ = r [cos( j - y )+j cosa sin(j - y + a )] - rf ; |
(1.48) |
Угол j для различных точек профиля эвольвент будет принимать следующие значения:
jp = jIII = 0; jH = jа = - tga; jIV = tgaa - tga .
Переходная поверхность формируется при нарезании зубьев, поэтому ее геометрия зависит от типа и геометрии применяемого инструмента, а также от параметров станочного зацепления. Ниже рассмотрена геометрия переходной кривой, подучаемой при использовании инструмента с кромкой зуба, очерченной дугой окружности радиусомrf, или прямой (фаской).
При нарезании колеса рейкой с угловыми точками профиля (с фаской) на вершине зубьев переходная часть профиля представляет собой траекторию угловой точки при обкатывании инструмента по делительной окружности нарезаемого колеса.
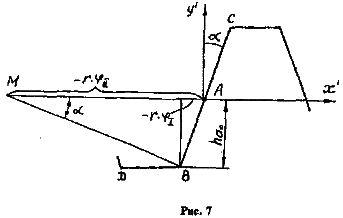
Выпишем в системе х' Ау' (рис.7) координаты угловой точки В режущей кромки зуба рейки:
x¢B = -ha0 × tga ; y¢B = -ha0 , где ha0 = h*a × m.
>Если подставить эти выражения в (1.48) для х и у, то получим уравнения искомой переходной кривой профиля:
| xB = -( ha0 tga + rj )cos( j - y ) + (-ha0 + r)sin( j -y ) ;
yB = -( ha0 tga + rj )sin( j - y ) + (-ha0 - r)cos( j -y )-rf . |
(1.49) |
Пределы изменения угла j определяют из следующих соображений. При отсутствии подрезания эвольвентная и переходная части профиля имеют плавное сопряжение в точке 3 (рис. 8), т.е. в этой точке у них имеется общая нормаль. Вершина В зуба рейки (см. рис. 7) касается эвольвентной части профиля зуба колеса в том положении обкатываемой рейки, когда точка М нормали к вершине В режущей кромки ВС рейки окажется лежащей на делительной окружности нарезаемого колеса. Основываясь на этом, имеем
![]()
Начальная точка I (см. рис. 5) переходной части профиля принадлежит одновременно и окружности впадин, причем в этой точке окружность впадин и переходная часть профиля имеют общую нормаль. Вершина В зуба рейки (см. рис. 7) касается в точке I окружности впадин в том положении обкатываемого инструмента, когда точка нормали к режущей кромке ВD оказывается на делительной окружности нарезаемого колеса. Осно-вываясь на этом, имеем
![]()
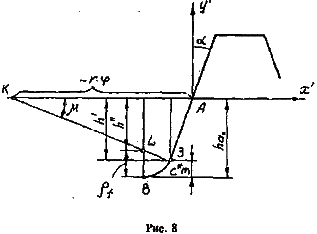
Рассмотрим теперь случай, когда рейка имеет закругления на вершинах. Произвольная точка 3 (см. рис. 8) закругления коснется переходной части профиля зуба колеса при таком положении обкатываемого инструмента, когда точка K нормали KЗ к закруглению окажется на делительной окружности нарезаемого колеса, т.е. когда точка Kстанет полюсом зацепления.
Высота закругления С=с* т (см. рис. 8), тогда радиус закругления rf будет найден из условия
![]()
Вместе с тем h¢ = ha0 - c*m, h² = ha0 - rf . Координаты точки L - центра закругления:
| xL¢ = -( h¢ tga + rf cosa );
yL¢ = -h² =-( ha0 - rf ), |
(1.50) |
координаты произвольной точки 3 закругления, определяемой угловым параметром m:
| x3¢ = xL¢ + rf cosm;
y3¢ = yL¢ - rf sinm . |
(1.51) |
Связь между параметрами m и j выражается зависимостью (см. рис. 8)
| (1.52) |
С учетом (1.48), (1.50) и (1.51) уравнение переходной кривой при наличии на зубьях рейки закруглений примет вид
|
x3 = -( h¢ tga + rf cosa - rf cosm +rj )cos( j - y ) + (- h¢ - rf cosm + r )sin(j - y ); y3 = ( h¢ tga + rf cosa - rf cosm +rj )sin( j - y ) + (- h¢ - rf sinm + r )cos(j - y ) - rf . |
(1.53) |
Пределы изменения угла j определяют из следующих соображений. В точке I (см. рис. 5) касания переходной части профиля с окружностью впадин угол m = 90°, отсюда следует, что
![]()
В точке II касания переходной и эвольвентной частей профиля угол m = a, откуда следует
![]()
Выведенные формулы справедливы и для случая нарезания колес червячной фрезой.