Общие условия синтеза планетарных механизмов

   При кинематическом синтезе многосателлитной планетарной передачи, конструируемой по заданной схеме, решают задачи подбора таких чисел зубьев ее колес, которые будут удовлетворять условиям: выполнения заданного передаточного отношения, правильности зацепления зубьев колес, соосности входного и выходного валов, соседства и сборки.

     Первые три условия являются общими при синтезе любой планетарной зубчатой передачи. Остальные диктуются особенностями кинематических схем планетарных механизмов.

     При синтезе планетарного механизма необходимо учитывать основные механические показатели качества: 1) КПД; 2) минимальные габаритные размеры; 3) массу проектируемого механизма;


4) динамические нагрузки в зацеплениях колес механизма, которые снижаются при выполнении следующих требований: а) числа зубьев центральных колес и числа сателлитов должны быть взаимно простыми; б) числа зубьев сопряженных колес не должны иметь общих множителей [4].

     При проектировании планетарного механизма силового привода необходимо оценивать его КПД до подбора чисел зубьев. В учебной практике можно воспользоваться рекомендациями табл. 3 или аналитическими зависимостями, приведенными в работе [4, с.79].

     Требования к габаритным размерам планетарного механизма обычно сводятся к тому, чтобы они не превышали заданных.

     Масса механизма зависит от многих факторов, однако в данном пособии учитывается только один из них; сумма чисел зубьев S всех колес механизма. Эту характеристику в дальнейшем и будем принимать за критерий оценки массы.

     Предположим, что схема механизма с учетом КПД выбрана, передаточное отношение и число сателлитов заданы. Все колеса имеют одинаковый модуль, который либо задан в исходных данных, либо может быть определен по формуле

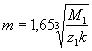(2.1)

где M1 - крутящий момент на входном звене; z1 - число зубьев центрального колеса; k - число сателлитов планетарного механизма.

     В этом случае проектирование сводится к подбору чисел зубьев колес. При решении этой задачи требуется учитывать следующие условия.

     1.  Сочетанием чисел зубьев колес должно с допустимой точностью обеспечиваться заданное передаточное отношение. При этом числа зубьев колес должны быть целыми числами.

     2.  При отсутствии специальных требований к габаритным размерам желательно использовать в планетарном механизме зубчатые колеса без смещений.

     Этими ограничениями учитывается отсутствие заклинивания передачи и подрезания зубьев: для колес с внешними зубьями, нарезанных стандартным инструментом, z ³ zmin = 17, для колес с внутренними зубьями в зависимости от параметров долбяка принимают z > zmin = 85 при h*a = 1 и z ³ zmin = 58 при h*а = 0,8.

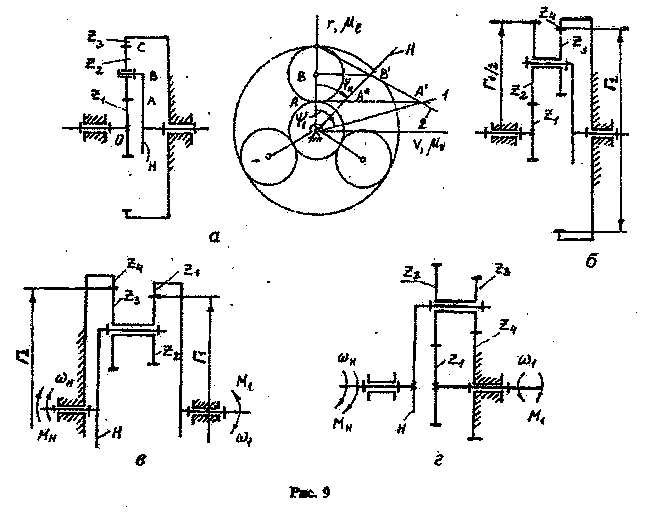
     3.  Условием соосности определяется соосное расположение центральных колес планетарного механизма с водилом H. Соосность основных звеньев приводит к равенству межосевых расстояний зацепляющихся колес. Для механизмов, изображенных на рис, 9, условие соосности можно конкретизировать в виде соотношений между радиусом водила и размерами радиусов начальных окружностей:

схема а: rH = rW1 + rW2 = rW3 - rW2 ;

схема б: rH = rW1 + rW2 = rW4 - rW3 ;

схема в: rH = rW1 + rW2 = rW3 + rW4 ;

схема г: rH = rW1 - rW2 = rW4 - rW3 .

 (2.2)

     4.  Условие совместности, или соседства, которое учитывает возможность свободного размещения сателлитов без соприкосновения их друг с другом. Это условие будет выполнено, если расстояние между осями сателлитов будет больше диаметра окружности вершин наибольшего сателлита  da2,3.  Математически это условие для механизмов, представленных на рис. 9, выражается неравенством

(2.3)

     В числителе правой часта неравенства (2.3) выбирают z2 в том случае, если   z2 > z3 , и наоборот, если z2 < z3 , то выбирают z3 . В знаменателе ставят относительное межосевое расстояние, т.е. если зацепление внешнее, то сумму чисел зубьев, если зацепление внутреннее - то разность чисел зубьев колес.

     Если необходимо определить наибольшее число сателлитов, которое может иметь планетарный механизм с известными числами зубьев, условие соседства приводят к виду

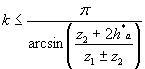 >(2.4)

     5.  Условие сборки с симметрией зон зацепления выражается соотношением

(2.5)

где k -  число сателлитов; Р = 0, 1, 2, 3 ... - целое число; Ц - любое целое число.

     Выполнение этого равенства фактически означает следующее: если один из сателлитов свободно устанавливается на вертикальной оси (рис. 10), то все последующие сателлиты будут свободно входить в зацепление с соответствующими колесами в той же позиции. Для этого необходимо повернуть водило на угол

(2.6)

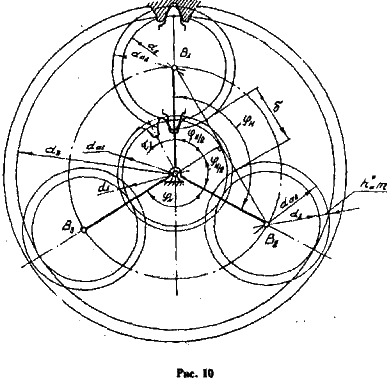
     У двухвенцовых сателлитов зубья одного венца одинаково ориентированы относительно зубьев второго венца.




Вернуться наверх