В исходных данных курсового проекта числа зубьев колес не заданы, и их необходимо определить на стадии проектирования кинематической схемы. Задача определения чисел зубьев сводится к составлению исходных уравнений, отражающих указанные условия и требования для каждой рассматриваемой схемы, и их совместному решению. Одним из простых методов определения чисел зубьев является метод сомножителей, при котором числа зубьев колес планетарного механизма определяют для заданного передаточного отношения, при правильном зацеплении зубьев колес (отсутствие подрезания зубьев и заклинивания передачи) и выполнении условия соосности. При этом проверяют условия сборки, соседства и учитывают конструктивные ограничения.
Планетарный двухрядный механизм со смешанным зацеплением (рис. 9, б). Дано: U1(4)H , k и m. Перепишем все ранее выведенные формулы и условия синтеза:
уравнение передаточного отношения
| (2.7) |
уравнение соосности
aW = rW1 + rW2 = rW4 - rW3
или при равных модулях во всех зацеплениях механизма
| z1 + z2 = z4 - z3 | (2.8) |
Уравнение (2.5) сборки имеет вид
![]()
Условие (2.3) совместности при z2 > z3 имеет вид
![]()
в случае, если z3 > z2,
![]()
Решение проводят методом сомножителей. Из уравнения (2.7) передаточного отношения определяют числовое значение (z2z4)/(z1z3) и полученное число раскладывают на сомножители А, В, С и D которым числа зубьев z1, z2, z3, z4 должны быть соответственно пропорциональны. Чтобы обеспечить соосность механизма aW1=aW2 , вводят дополнительные множители, поставленные в скобки:
С учетом условия соосности для этой схемы
z1 = A(D - C)q ;
z2 = B(D - C)q ;
z3 = C(A + B)q ;
z4 = D(A + B)q .
Общий множитель q подбирают так, чтобы все числа зубьев были целыми и z1 > 17; z2 > 17; z3 ³ 20; z4 ³ 85, а z4 - z3 ³ 8.
Затем следует проверить, как выполняются условиясборки (2.5), соседства (условие (2.3)) и требования к габаритным размерам.
Планетарные двухрядные механизмы с двумя внешними (рис. 9, г) или двумя внутренними (рис. 9, в) зацеплениями. Для указанных схем планетарных механизмов ведущим звеном является водило U1H = wH / w1 . При решении задачи полагают заданными U1H, k и т.
Выписывают необходимые уравнения:
уравнение передаточного отношения
| (2.10) |
>уравнение соосности
| rW1 + rW2 = rW3 + rW4 или z1 + z2 = z4 + z3 | (2.11) |
(знак плюс соответствует внешнему зацеплению, знак (минус) соответствует внутреннему зацеплению);
уравнение сборки
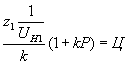
условие соседства
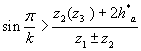
Решение проводят методом сомножителей.
Из уравнения (2.10) определяют числовое значение отношения, которое заменяют отношением, составленным из сомножителей А, B, C и D, соответственно пропорциональных числам зубьев: BD/AC=(1 - 1/UH1) .
Чтобы обеспечить соосность двухрядного планетарного механизма ( aWI = aWII ), числа зубьев подсчитывают по формулам
|
z1 = A( D + C )q ; z2 = B( D + C )q ; z3 = C( A + B )q ; z4 = D( A + B )q . |
(2.12) |
Последним этапом решения задачи синтеза является проверка по условиям сборки и соседства.
Однорядный планетарный механизм (рис. 9, а). Дано: U1H, k и т. Выписывают все необходимые уравнения:
уравнение передаточного отношения
| (2.13) |
уравнение соосности для заданной схемы механизма rW1 + 2rW2 = rW3. Если зубья колес планетарного механизма без смещений, то z1 + 2z2 = z3;
уравнение сборки
| (2.14) |
условие соседства имеет вид
![]()
Далее решение проводят в такой последовательности:
1. Задают число зубьев центрального колеса z1 > zmin = 17.
2. Из уравнения (2.13) определяют z3 = z1( U1H - 1). Число зубьев опорного колеса z3 должно быть целым числом, большим 85.
3. Из уравнения соосности (2.14) определяют z2 = ( z3 - z1 )/2
Число эубьев у сателлита должно быть целым числом, большим или равным 20.
4. Проверяют условие сборки по уравнению (2.5):
![]()
5. Проверяют условие соседства по неравенству (2.3):
Если хотя бы одно из условий не выполняется, то следует выбрать другое значение x1.
После определения чисел зубьев планетарного механизма и расчета радиусов делительных окружностей колес на листе изображают кинематическую схему механизма в двух проекциях и на одной из них строят треугольники скоростей (см. рис. 3, б). Угловые скорости колеса z1 и водила Н пропорциональны тангенсам углов y1 и y2; передаточное отношение U1H =w1/wH = tgy / tgyH = AA¢/AA² Углы y1 и y2 однозначны, следовательно, и угловые скорости будут иметь одинаковое направление.